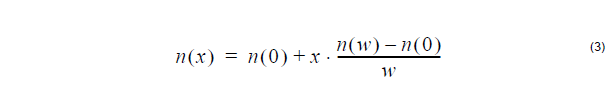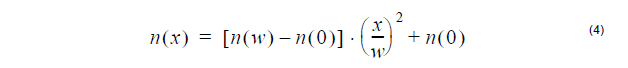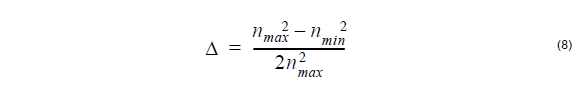Refractive Index of Fibers

Host materials

Optical telecommunication-grade fibers are made usually from silica glasses. The
high purity glass is called the host material or substrate. Its bulk refractive index
usually defines the refractive index of the fiber cladding. Adding dopant materials to
the host material forms the fiber core.

Dopant materials

To change the refractive index of optical fiber, pure silica is often doped with dopants.
For example, adding germanium can result in an increase in the refractive index,
while adding fluorine reduces it. The refractive index of doped material can be
determined by the linear relationship between the doped material’s mole percentage
and permittivity.

Aumme that n₀ is the refractive index of the host material and n₁ is the refractive index
of m₁ molepercentage doped material. Then, the refractive index n of m molepercentage
doped material can be interpolated as:

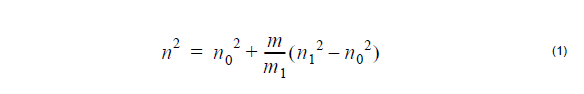The radial distribution of the fiber refractive index is called the index profile. That
profile determines guiding properties of the fiber. In general, the core region has a
higher index than the cladding region. However, the index profile can have regions
where the index is lower than the cladding value. Modern fiber designs are based on
index profiles that assure proper operation within a range of wavelengths.

For example, a dispersion flattened fiber design involves a couple of concentric index
regions.

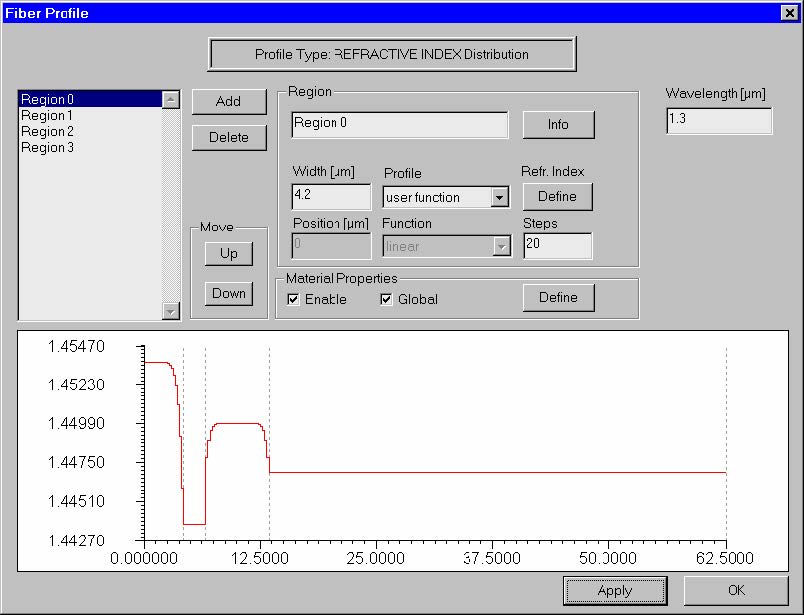
In OptiFiber “regions” define a rotationally symmetric fiber profile. In the picture
above, the fiber profile consists of four regions. Each region has its dimension (width)
and profile. The default profile options are listed below, where x is the region’s local
coordinate, w is the width of the region.

Constant profile: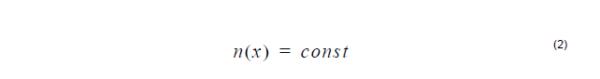Linear profile:

Parabolic profile:

Exponential profile:

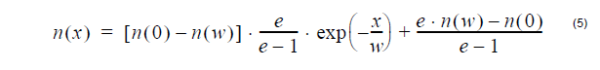where n(0), n(w) is the refractive index at x = 0 and x = w, respectively.

Gaussian profile:

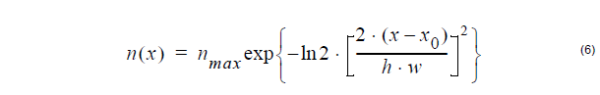where n_max is the maximum value, x₀ is the peak position, and h is the
normalized value of FWHM.

Alpha –peak profile:

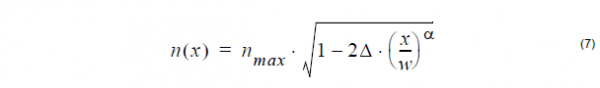where n_max is the maximum value, Δ is normalized difference. It is defined as:

Alpha –dip profile:

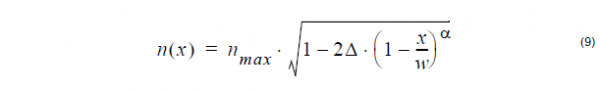where n_max is the maximum value, Δ is normalized difference.

Two techniques for defining the refractive index profile

Currently OptiFiber implements two methods for defining the geometry and the
material composition of the fiber:

• Direct definition of the refractive index profile: the abscissa values n(x) in the
  formulae above are interpreted directly as refractive index values at a user
  specified wavelength. Wherever needed, the dopant concentration in each region
  is internally calculated by interpolating the given value between the refractive
  index values of two materials – “Dopant +” and “Dopant -” and using the formula
  given in “Dopant Materials”. The material dispersion and dispersion of the profile
  are calculated from the known Sellmeier coefficients of “Dopant +” and “Dopant –
  ”. The parameters of the materials “Dopant +” and “Dopant -” are either taken from
  the internal extendable material library of OptiFiber or user specified. They can
  be different for each region or global for the whole profile. This method is
  convenient whenever the distribution of the refr. index is known from experimental
  measurements, estimations, etc.
• Definition of a dopant concentration profile: the abscissa values n(x) in the
  formulae are interpreted as molar concentration of a certain dopant. The material
  dispersion and dispersion of the profile are calculated from the known Sellmeier
  coefficients of the dopant, which are taken from the internal extendable material
  library of OptiFiber or are user specified.

This method is convenient when the dopant concentration distribution of the fiber or
at least of its preform are known with sufficient accuracy.