Using recurrence formula Equation 118 for Padé (4,4) we get:
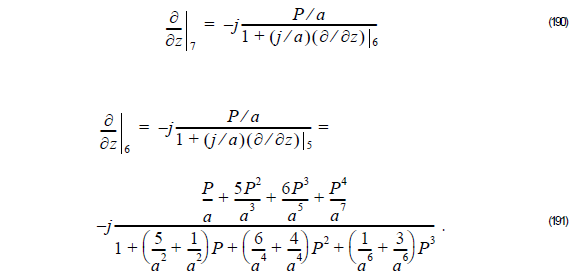
Using Equation 191 into Equation 190 we get:
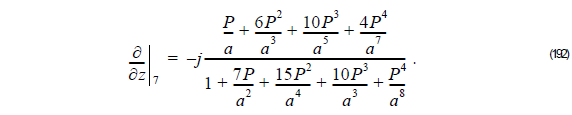
From Equation 192, we get:
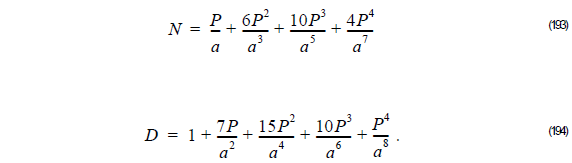
Thus,
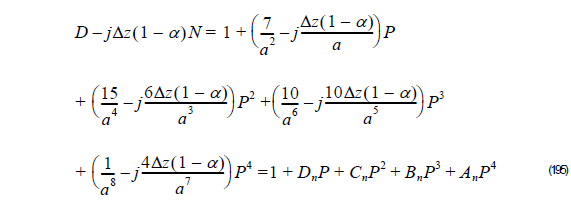
and
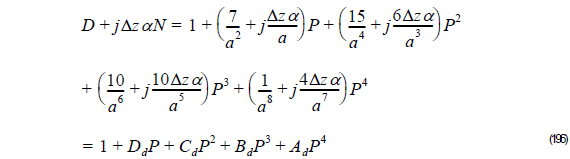
here
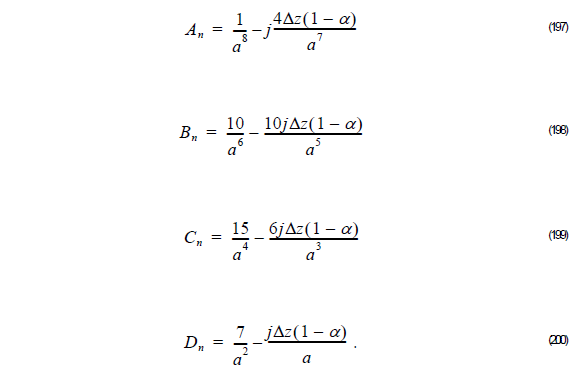
Thus, the unknown field φ l + 1 at z + Δz is related to the unknown field φ l at z as follows:
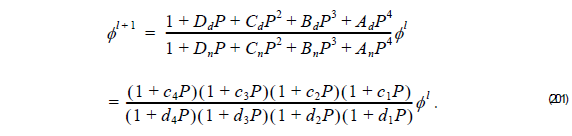
Multistep Method
In order to solve Equation 201, we use the multistep method, that is, the unknown field
φ l + 1 is obtained with the following the steps:
1 Compute φ l + 1 ⁄ 4 solving the linear system:
![]()
In case of using FEM compute,
![]()
2 Compute φ l + 1 ⁄ 2 solving the linear system:
![]()
In case of using FEM compute,
![]()
3 Compute φ l + 3 ⁄ 4 solving the linear system:
![]()
In case of using FEM compute,
![]()
4 Finally, knowing φ l+ 3 ⁄ 4, compute the known field φ l + 1 at z + Δzl solving linear system:
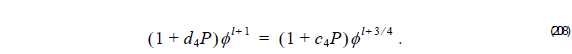
In case of using FEM compute,
![]()
The advantage of the multistep is that the matrix equation to be solved in each step is the same size as the Fresnel equation and for 2D problems is tridiagonal when we consider Finite Difference method (FD) or Finite Element Method (FEM) considering linear element.

