| Step |
|
| 1 |
Now, open a new project with File > New > Single Fiber. |
| 2 |
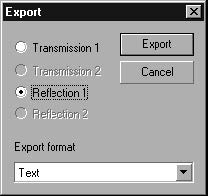
Choose Calculation > Inverse Scattering Solver to get the Inverse Problem Solver dialog box. |
| 3 |
Select the From File checkbox. |
| 4 |
Navigate to the place where you left the file with the reflection spectrum. Open the file.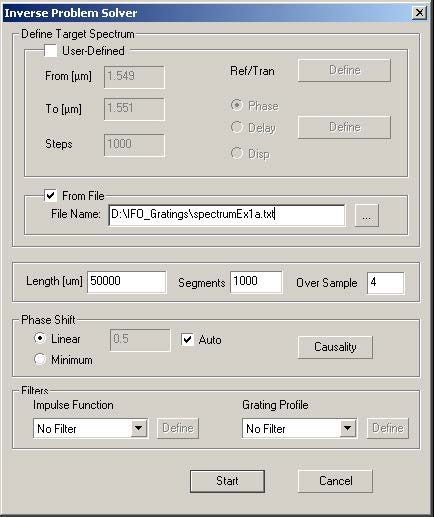 |
| 5 |
We suppose that the original length of the grating is known, so enter 50000 μm in the Length box. (Feel free to experiment with different lengths.)
- The original spectrum was generated with a profile having 100 segments. It is not necessary that the reconstruction have the same number, here it is set to 1000.
|
| 6 |
Click on the Causality button to test this spectrum.
- Since this spectrum was generated from a real grating, it displays exactly the causal property of being zero for negative argument.
|
| 7 |
Click Close. |
| 8 |
Click Start in the Inverse Problem Solver dialog box to begin the
reconstruction. |
| 9 |
Click on Spectrum to enable all tabs. |
| 10 |
Select the Profile tab to see the reconstructed profile.
- The apodization appears to be a similar shape as the original grating.
|
| 11 |
To see the chirp more clearly, right click the mouse in the Profile window and select Chirp Period.
. . . to get the following:
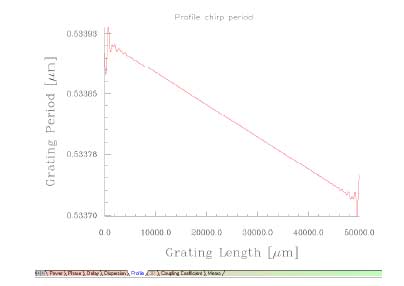
- The chirp is linear and shifts by 0.2 nm, like the original grating.
|
| 12 |
Select the Power tab to compare the reflectivities, one from the imported complex spectrum and the other from the calculated response of the reconstructed grating.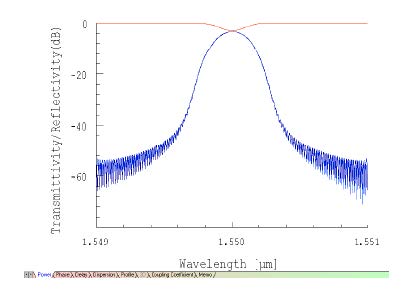 |