In the absence of electrode fields the refractive index ellipsoid, or indicatrix, is of the following form:
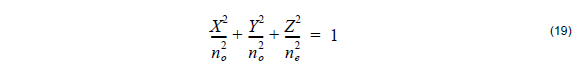
where no , ne are the ordinary and extraordinary refractive indices, respectively.
Under the influence of an electric field the index ellipsoid is deformed in space:

In different cases of the cut, the propagation and polarization, and the electrode field direction, different electrooptic coefficients rij are used in the simulation program. Table 4 is the reference table to help you in entering your electrooptic coefficients. The mixed coupling terms in the index ellipsoid were ignored. The change in the corresponding refractive index can be approximated as
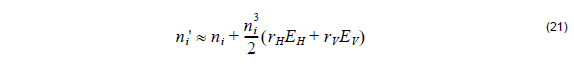
where EH , EV , rH , and rV are the electric fields in horizontal and vertical directions and the corresponding electro optic coefficients, respectively, and i denotes either ordinary or extraordinary refractive index. Notice that whether the electrode field is considered horizontal or vertical depends on the electrode configuration, voltage and the waveguide position. Intuitively, you can assume that the electrostatic field lines between electrodes follow patterns familiar from electrostatics. For example, if you place one of the electrodes right on the top of the waveguide, it will likely produce the static field that is vertical in the waveguide.
|
TE |
TM |
||||
| Crystal Cut | Propagation
Direction |
Horizontal
Electrode Field |
Vertical
Electrode Field |
Horizontal
Electrode Field |
Vertical
Electrode Field |
| X | Y | r33 | 0 | r13 | 0 |
| Y | X | r33 | 0 | r13 | r22 |
| Z | X | r22 | r13 | 0 | r33 |
| Z | Y | 0 | r13 | 0 | r33 |
| Y | Z | 0 | –r22 | 0 | r22 |
| X | Z | r22 | 0 | –r22 | 0 |
Table 4

