This lesson demonstrates the basic effects of self-phase modulation (SPM) on pulse propagation. These include:
- Pulse chirping
- Pulse spectral broadening
The effects SPM of are described by [1]:

where E(z, t) is the electric field envelope, and the parameter y is given by:

In Equation 2, ω0 is the carrier (or reference) frequency, n2 is the nonlinear-index
coefficient and Aeff is the effective core area [1].
The straightforward solution of Equation 1:
E(z, t) = E(z = 0, t)exp(i |E(z = 0, t)|2)
shows that the pulse shape (i.e. |E(z, t)|2 = |E(z = -, t)|2) remains unaffected by
SPM. The temporarily varying phase |Φ NL = | E(z = 0, t)|2z implies that the
instantaneous optical frequency across the pulse is different from the carrier
frequency ω0 . The frequency difference δω(t) is given by [1]:

and the time dependence of δω(t) is referred to as frequency chirping. While the
action of GVD also yields pulse chirping, the chirp associated with SPM has an
entirely different origin – in the latter case, new frequency components are generated
that result in spectral broadening, while the spectrum remains unaffected by GVD.
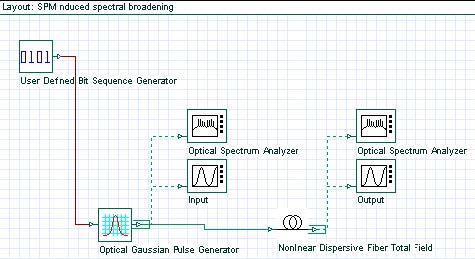
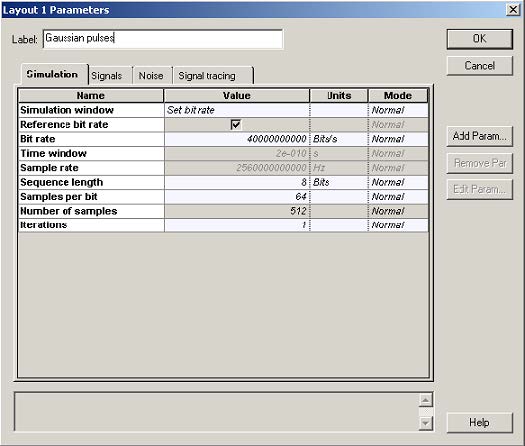
To demonstrate the effect of SPM we can use the following layout (Figure 1). In the
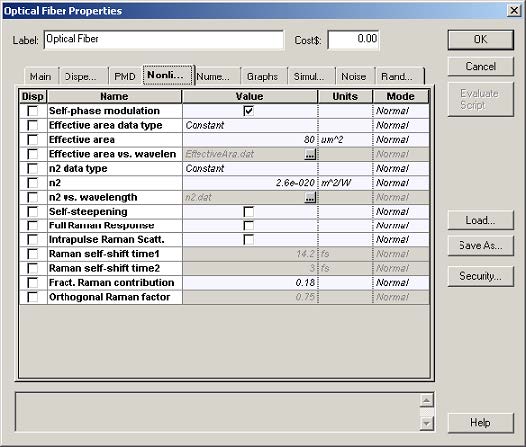
Nonlinear Dispersive Fiber Total Field component properties, we disable all the effects
except SPM (see Figure 2).
With the values of the parameters shown in Figure 2, the value of y is y = 1.317W–1km–1.
Figure 1: Layout of SPM induced spectral broadening and parameters
Figure 2: Setting the “nonlinearities” tab to observe the effects of SPM
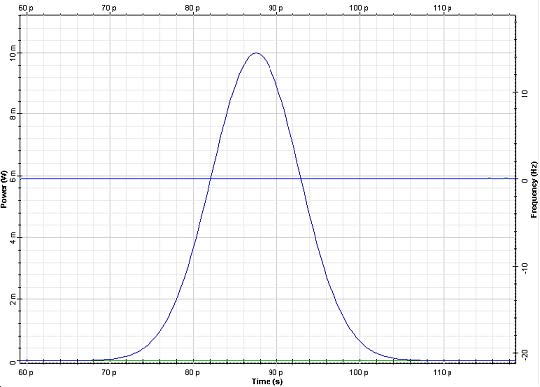
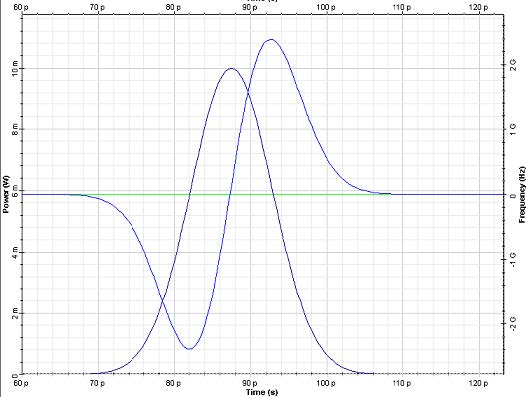
With the pulse peak power equal to 10 mW and the fiber length to 10.73 km, the obtained results are shown in Figure 3. The pulse shape remains unchanged and the output pulse is chirped. Note that the sign of the chirp is reversed compared to the case of dispersion-induced pulse chirping in the case of anomalous GVD.
Figure 3: Input (left) and output (right) pulse shape and chirp with propagation distance of 10.73 km
In Figure 3, the leading edge of the pulse becomes red-shifted and the trailing edge of the pulse becomes blue-shifted. If the effects of anomalous dispersion were present, with the chirp induced by SPM some pulse narrowing would occur. This means that the effect of SPM counteracts GVD.
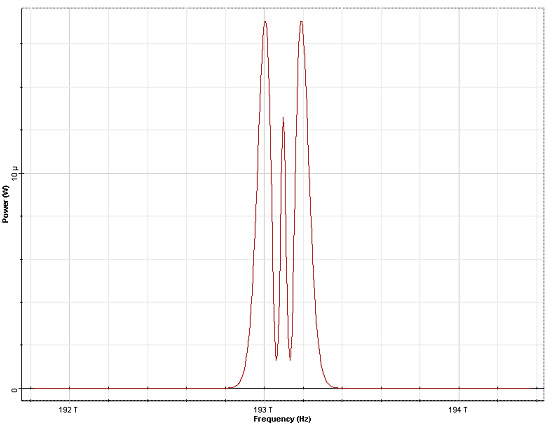
To see the SPM induced spectral broadening let us introduce the quantity
φmax = yP0z where P0 is the peak power. Figure 4 shows the spectra for an
unchirped Gaussian input pulse for several values of the maximum phase shift.
The effects of SPM-induced chirping and spectral broadening are related [1]. According to Figure 3, the same chirp occurs at two values of t which means that the instantaneous frequency is one and same at two distinct points. These two points represent two waves of the same frequency that can interfere constructively or destructively producing, thus, the oscillatory structure of the pulse spectrum.
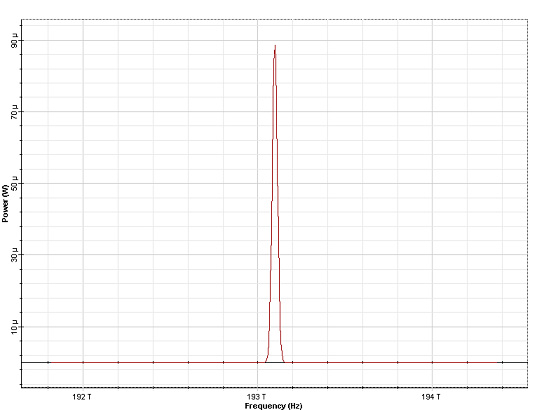
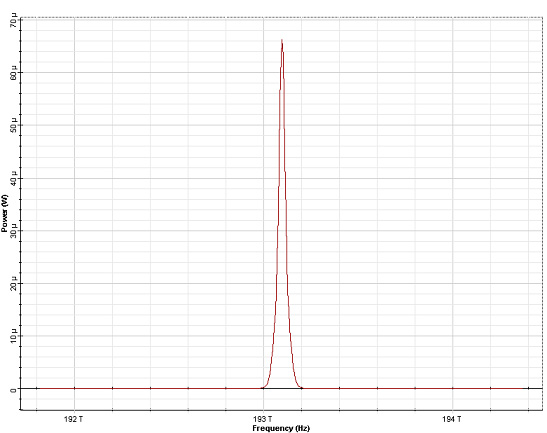
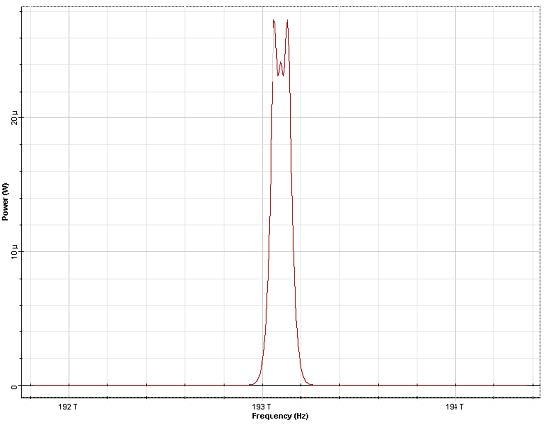
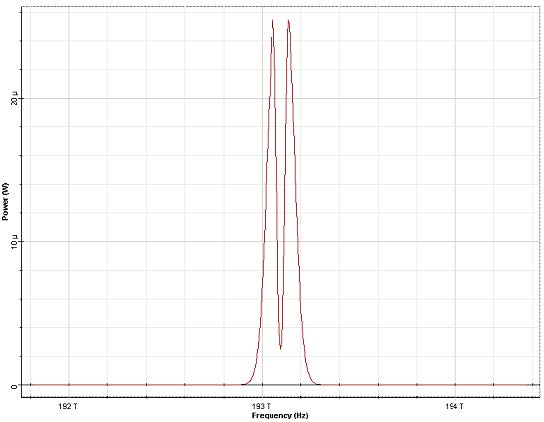
Figure 4: SPM broadened spectra for an unchirped Gaussian pulse
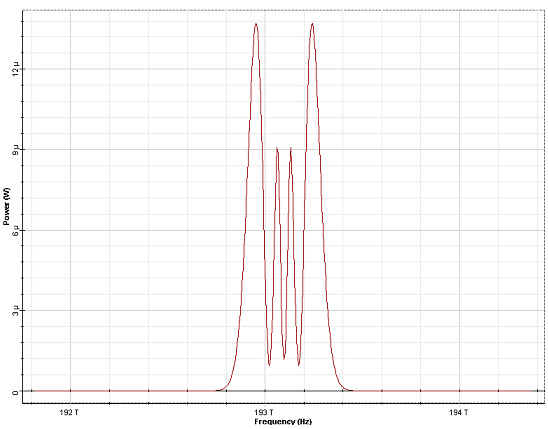
The SPM induced spectral broadening depends on the pulse shape and on the initial chirp. The dependence on the pulse shape is shown in Figure 5 where the output spectra of Gaussian and super-Gaussian (third order) pulses are presented for φmax = 4.5π :
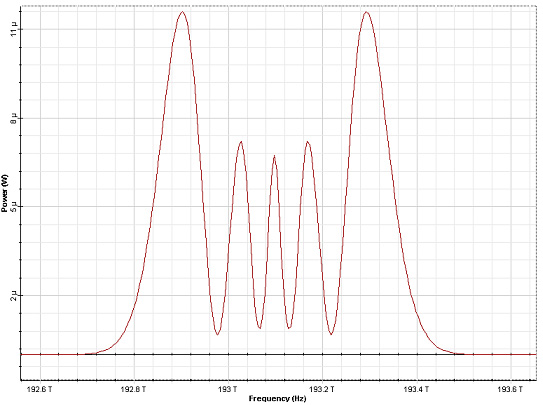
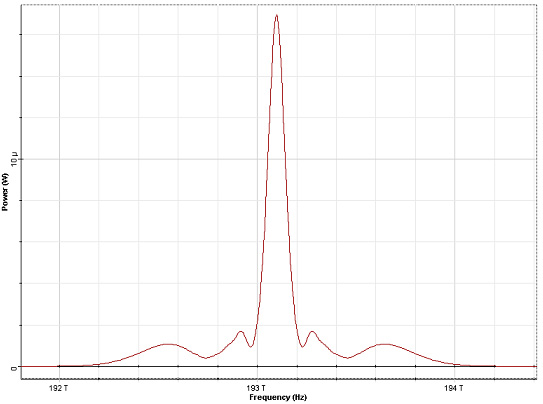
Figure 5: SPM broadened pulse spectra at φmax = 4.5π
References:
[1]G. P. Agrawal Nonlinear Fiber Optics, Academic Press (2001).