To demonstrate the influence of the group (GVD) velocity dispersion on pulse propagation in optical fibers in “linear” regime. The basic effects related to GVD are:
- GVD induced pulse broadening
- GVD induced pulse chirping
- Pulse compression
The equation, which describes the effect of GVD on optical pulse propagation neglecting the losses and nonlinearities, is [1]:

where is the propagation direction, is the time, is the electric field envelope, and
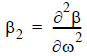
is the GVD parameter, defined as the second derivative of the fiber mode propagation constant with respect to frequency.
For an input pulse with a Gaussian shape,
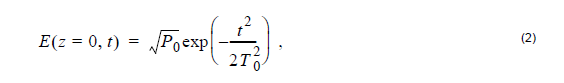
the pulse width T0(related to the pulse full width at half maximum by
TFWHM ≈ 1.665T0) increases with z (the pulse broadens) according to [1]:

and, consequently, the peak power changes, due to GVD, are given by:
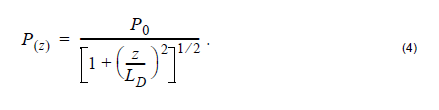
In Equation 3 and Equation 4, the quantity
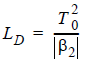
is the dispersion length.
Its meaning is quite straightforward: after propagating a distance equal to LD, the pulse broadens by a factor of √2.
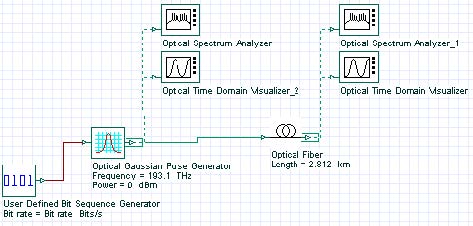
To demonstrate this, we created the following simple project (Figure 1).
Figure 1: GVD project layout
We set the Bit rate equal to 40 Gb/s, which corresponds to bit duration of 25 ps. Using
the default value of 0.5 for “width” of the Optical Gaussian Pulse Generator, the
resulting FWHM of the pulse is 12.5 ps.
The T0 parameter is then
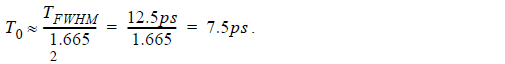
Using the value of β2 ≈ -20(ps)2 at 1.55μm for SMF, the dispersion length is:
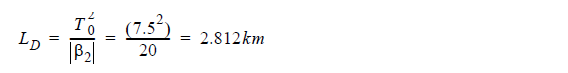
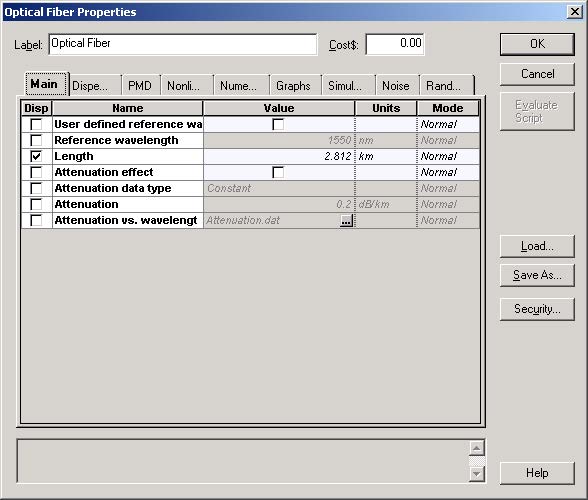
In the Optical Fiber properties, we set the length of the fiber equal to this value, and
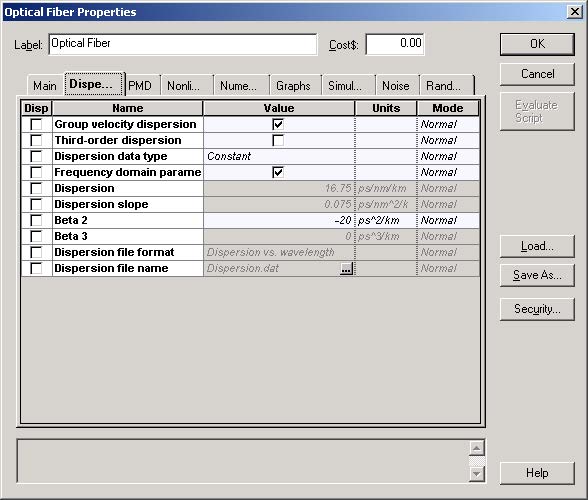
we disable all the effects except GVD (Figure 2).
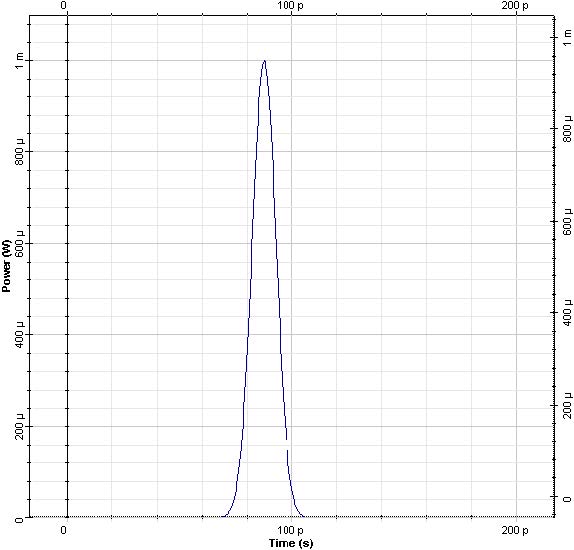
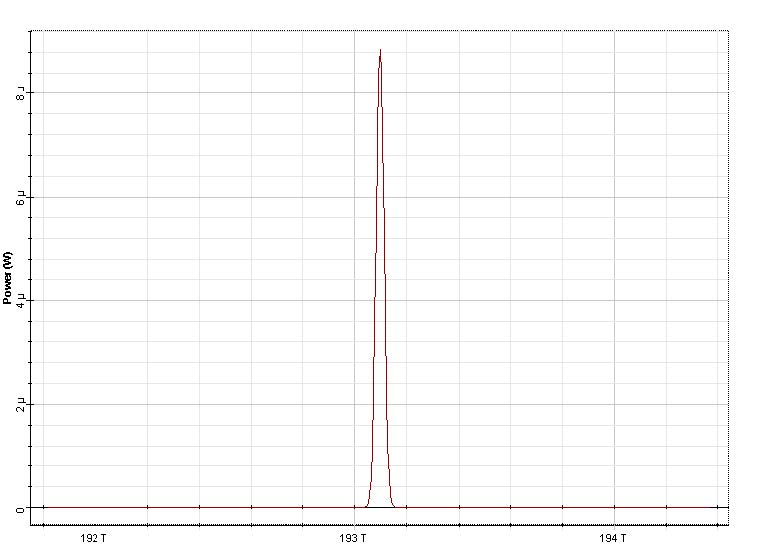
We calculate the project and the obtained results are presented in Figure 3. We see that the pulse is broadened (the peak power decreases in accordance with Equation 4). The origin of pulse broadening can be understood be looking at the instant frequency of the pulse, namely the chirp.
Figure 2: Optical Fiber properties
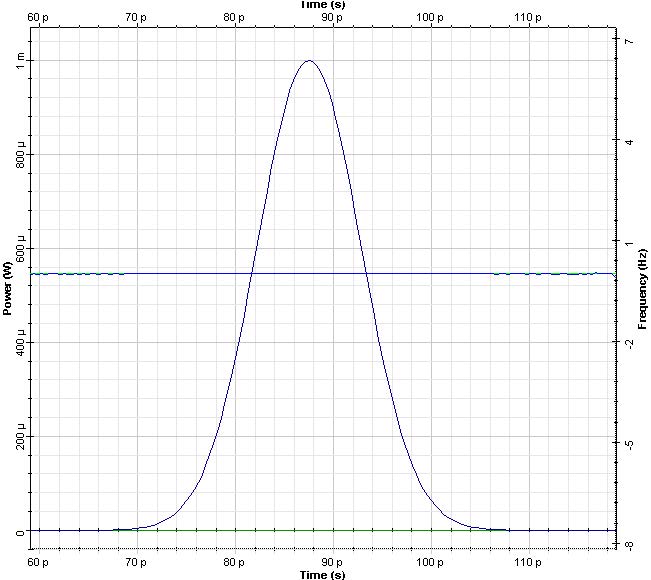
This is shown in Figure 4, where the pulse chirp is plotted together with the pulse intensity. Whereas the input pulse is chirpless, the instantaneous frequency of the output pulse decreases from the leading to the trailing edge of the pulse. The reason for this is GVD. In the case of anomalous GVD (β2 < 0), the higher frequency (“blue-shifted”) components of the pulse travel faster than the lower frequency (or “red-shifted”) ones [1].
Figure 3: Left plot – input pulse, right plot pulse at
Figure 4: Same as in Figure 3. The straight lines represent the chirp
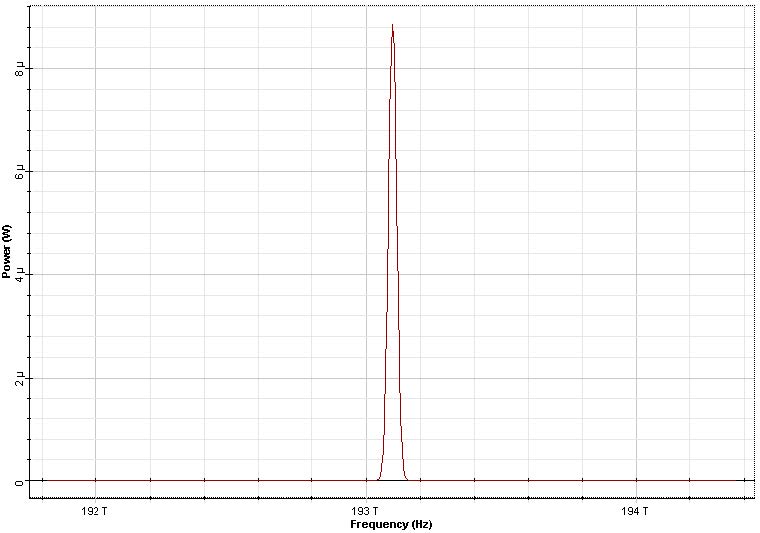
Note: The leading edge of the pulse is blue shifted and the trailing edge of the pulse is red-shifted. Because the “blue” and “red” spectral components tend to separate in time, this leads to pulse broadening. However, the pulse spectrum remains unchanged, as Figure 5 shows.
Figure 5: Input (left plot) and output (right plot) spectra corresponding to Figure 3 and 4
If the input pulse is frequency modulated (i.e. chirped), Equation 2 is replaced by:
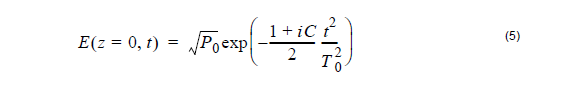
and the expression for the dependence of the pulse width on z is [1]
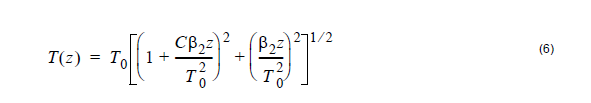
The pulse broadens monotonically with z if β2C > 0 , however, it goes through initial
narrowing when . In the latter case, the pulse width becomes minimum at
distance [1]:

and is given by

The peak power of the pulse in this case is:
P(zmin) = P0(1 + C2)1/2
Initial narrowing of the pulse for the case β2C < 0 can be explained by noticing that
in this case the frequency modulation (or “chirp”) is such that the faster (“blue” in the
case of anomalous GVD) frequency components are in the trailing edge, and the
slower (or “red” in the case of anomalous GVD) in the leading edge of the pulse. As
the pulse propagates, the faster components will overtake the slower ones, leading to
pulse narrowing. At the same time, the dispersion induced chirp will compensate for
the initial one. At z = zmin , full compensation between both will occur. With further
propagation, the fast and the slow frequency components will tend to separate in time
from each other and, consequently, pulse broadening will be observed.
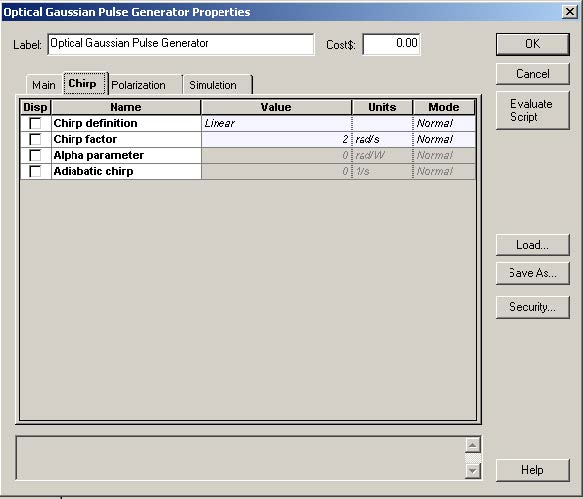
To demonstrate this, we use a chirped Gaussian pulse with the chirp parameter C = 2 (since β2 < 0 in our case) (Figure 6).
Figure 6: Setting the chirp parameter to observe pulse compression
Using Equation 7 and Equation 9, we obtain:
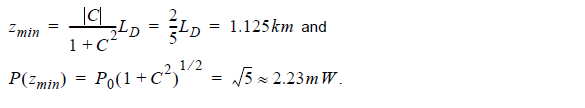
We change the length of the fiber to 1.125km and calculate the project.
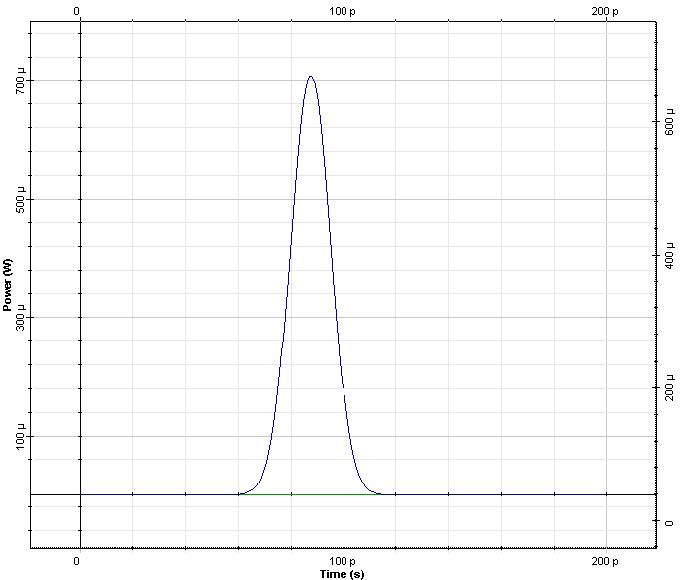
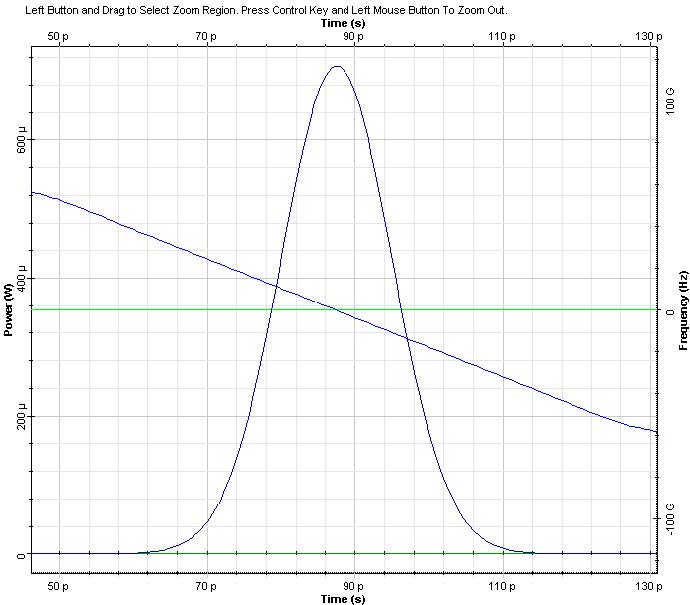
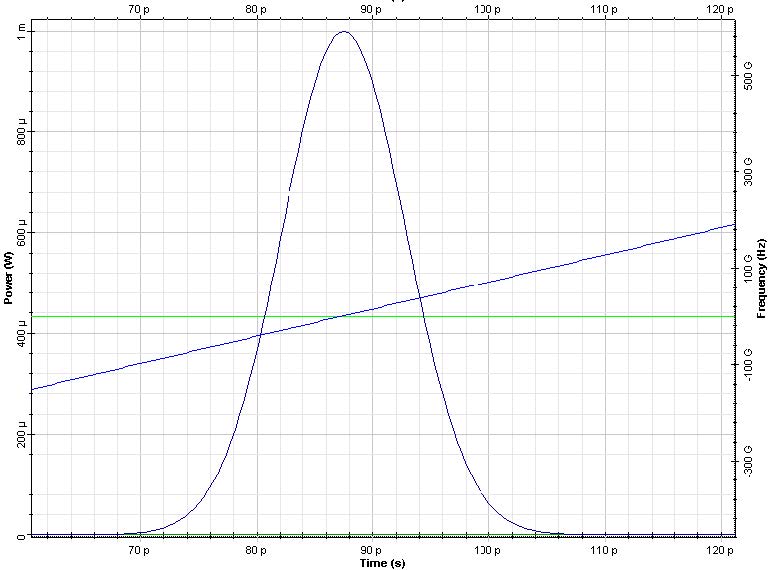
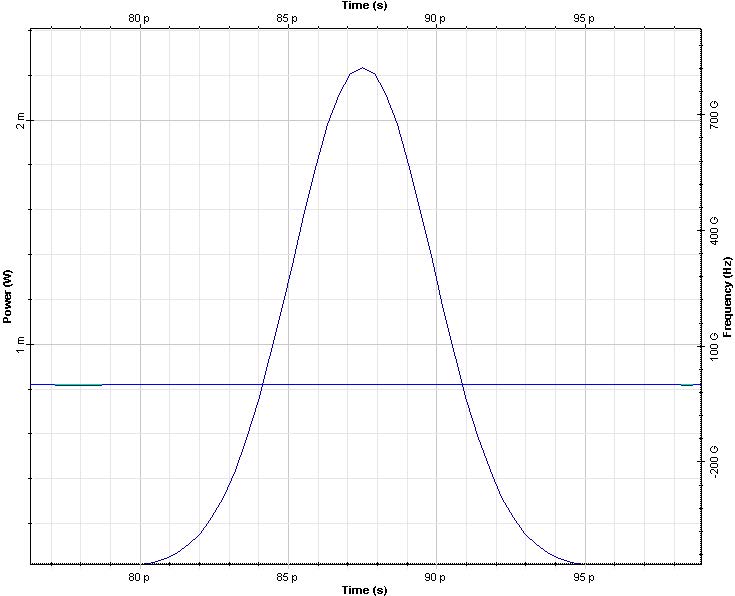
The results for the output pulse shape and chirp are presented in Figure 7. It can be seen that an exact compensation between the dispersion induced and initial chirp occurs, and that the peak power of the pulse is 2.2mW, as given by Equation 9.
Figure 7: Pulse shape and chirp at z=0 (left) and z=zmin (right)
Note: There is exact compensation between the initial and the dispersion-induced chirp.
Reference:
[1]G. P. Agrawal Nonlinear Fiber Optics, Academic Press (2001).