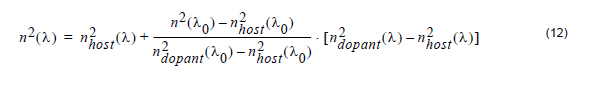Material refractive index varies with wavelength and therefore causes the group
velocity to vary; it is classified as material dispersion. The wavelength dependence of
refractive index can be expressed by Sellmeier’s equation. Waveguide dispersion is
the result of wavelength-dependence of the propagation constant of the optical
waveguide. It is important in single-mode waveguides. The larger the wavelength, the
more the fundamental mode will spread from the core into the cladding. This causes
the fundamental mode to propagate faster. The material and waveguide dispersion
effect is important when the grating filter has a broadband response, such as a codirectional waveguide coupler and a long period fiber grating. In these cases, the
waveguide mode constants are re-calculated for different wavelength by considering
material dispersion.
Host materials
Optical telecommunication fibers are usually made from silica glasses. The high purity
glass is called the host material or substrate. Its bulk refractive index is usually the
fiber cladding refractive index. The fiber core is formed by adding dopant materials to
the host material.
Dopant materials
To change the refractive index of optical fiber, pure silica is often doped with dopants.
For example, adding germanium can result in an increase in the refractive index,
while adding fluorine reduces it. The refractive index of doped material can be
determined by the linear relationship between the doped material’s mole percentage
and permittivity.
Assume that n0 is the refractive index of the host material and n1 is the refractive
index of m1 mole-percentage doped material. Then, the refractive index n of m molepercentage doped material can be interpolated as:
Note that this formula can also extrapolate (the case where m > m1 )
Material dispersion calculation
In OptiGrating 4.2, when the refractive index at a central wavelength λ 0, n(λ0) and
the host and dopant material dispersion curves, nhost(λ) and ndopant(λ) are
defined, the dependence of the refractive index with wavelength, n(λ), is calculated
based on the following equation:
This equation is the same as (11), with the fraction m/m1 estimated by comparing,
at the centre wavelength λ0, the refractive index of the given material with the index
of a doped material with known Sellmeier coefficients ndopant. OptiGrating uses
Equation 12 to handle the case where the Sellmeier coefficients are known for
material of just one doping concentration. If the material in question has the same
dopant, but with an unknown concentration, the fraction in Equation 12 will estimate
the concentration by comparing the given index n(λ0) with the reference index
ndopant(λ0). With the doping concentration estimated this way, the refractive index
at other wavelengths is accurately estimated by Equation 12. On the other hand, in
the case where the Sellmeier coefficients are exacly known for the given material, the
user can enterthem himself in OptiGrating’s Sellmeier Coefficient Library. OptiGrating
still uses Equation 12, since in this case the fraction is calculated as unity, and the left
hand side is assigned to ndopant(λ0) for all wavelengths directly.