As we know, the periodic structure or the lattice structure has the mode selection
function. The task of the band solver is to find these mode positions based on one or
several basic lattice cell. The key points for FDTD simulation come from:
- How can the FDTD method extract the mode?
- How can the FDTD method handle several basic cells and generate global results?
The first question can be addressed in two parts:
- set the reasonable initial fields that can excite out all necessary modes
- get the eigenvalues (frequencies) from the Fourier spectrum of the field time sequence somewhere in the periodic cell.The second question can be solved by using the Bloch’s boundary condition with defined k-vector.
In summary, when a field pattern is excited in the first time step, the steady state
oscillating mode which will satisfy the Bloch’s boundary condition will be found
through FDTD simulation in the defined periodic cell.
Note:
- To extract all the excited eignevalues, observation points to record the time domain series are needed.
- Some of the mode may not be excited.
- Because of the above points, the FDTD band solver cannot be guaranteed to find all the eigenvalues.
Basic equation for TE mode 2D simulation
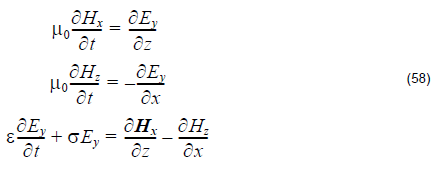
Basic equation for TM mode 2D simulation
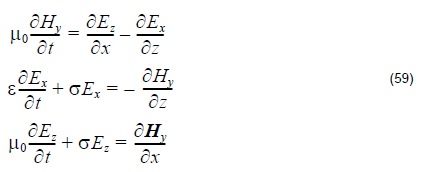
Note:
- The above equations are same as the equations used in conventional FDTD simulations. However, because the Bloch’s boundary condition is used in the simulation, all the field components in band solving are complex values.
- The discretization treatment for the FDTD method and simulation domain is same as conventional FDTD simulation.

