The Maxwell equation in a transparent, time-invariant, source free, and non-magnetic
medium can be written in the following form:
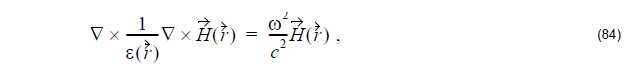
where ε(![]() ) is the space dependent dielectric function, c is speed of light in vacuum,
) is the space dependent dielectric function, c is speed of light in vacuum,
and ![]() is the optical magnetic field vector of a definite frequency ω with time
is the optical magnetic field vector of a definite frequency ω with time
dependence eiωt . This equation is sometimes called the master Equation 84, and
represents a Hermitian eigen-problem, which would not be applicable if the wave
equation were derived in terms of the electric field.
The Bloch theorem says that, due to the infinite periodicity, the magnetic field will take
the form:

where ![]() for all combinations of lattice vectors
for all combinations of lattice vectors ![]() . Thus, we end up
. Thus, we end up
with the master equation in operator form:
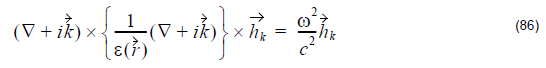
This is the fundamental equation, which needs to be solved. The equation is
transformed into a finite problem by expanding the magnetic field in a finite basis of
simple plane waves. Different approaches can be explored to solve the final
discretized problem, e.g. (85) and (86). The result of solving the discretized problem
is the dispersion relationship between the frequencies of the modes and wave vector
![]() , usually plotted in the form of a band diagram.
, usually plotted in the form of a band diagram.

