It has been shown [1] that a complex dielectric function for some metals and surface
plasmas can be expressed in the following form:

This form separates explicitly the intraband effects (usually referred to as free electron
effects) from interband effect (usually referred to as bound-electron effects). The
intraband part εfr ( ω ) of the dielectric function is described by the well known free electron or Drude model [2][3]:

The interband part of the dielectric function is described by the simple semi quantum
model resembling the Lorentz results for insulators:
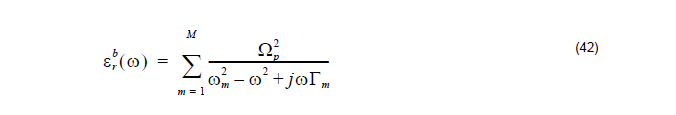
where ωp is the plasma frequency, m is the number of oscillators with frequency ωm
and lifetime 1 / Γm , where Ωp = √Gm ωp is the plasma frequency as associated
with intraband transitions with oscillator strength G0 and damping constant Γ0.
The above Lorentz-Drude Model can be expressed as the more general equation:
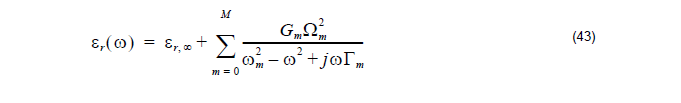
where εr,∞ is the relative permittivity in the infinity frequency. Ωm is the plasma
frequency, ωm is the resonant frequency, and Γm is the damping factor or collision
frequency.
In this general equation, if only the term m = 0 exists, and ω0 = 0, then the
general equation describes the Drude model as in (41). If only the m = 1…M term
exists, and Ω1 = Ω2 = … = Ωm ; then the general model becomes the Lorentz
model as in (42). This model can also work as the separate Drude and Lorentz
models.
Reference [1] also gives the LD parameters for 11 noble metals; their unit is in electron volts. The OptiFDTD Material Library manual can be found in the documentation folder after installation, it contains parameters compiled by Optiwave that describe noble metals and other dispersive materials.

