Bloch’s theorem tells us that for periodic structure, field components have the
following properties:
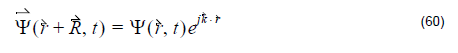
where R is the lattice vector, k is the wave vector. Equation 60 is the boundary
condition used in the OptiFDTD band solver.
Initial excitation
Unlike conventional FDTD simulations where time domain excitation is continuous
wave and lasts on only some time steps, the FDTD band solver sets the initial value
in the first time step, and this initial field is expected to have non-zero projection on
the normal modes we are interested in.
Example: At t = 0 :
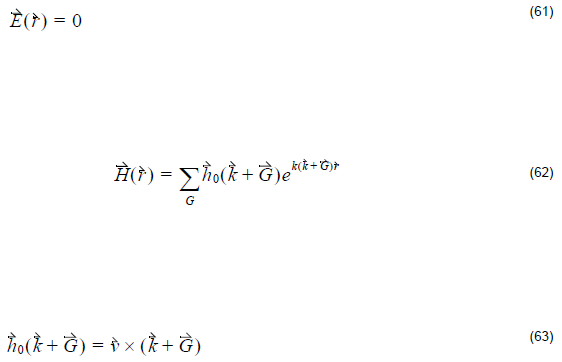
![]() is chosen as the unit vector along the Cartesian system coordinator.
is chosen as the unit vector along the Cartesian system coordinator.
This keeps ![]()
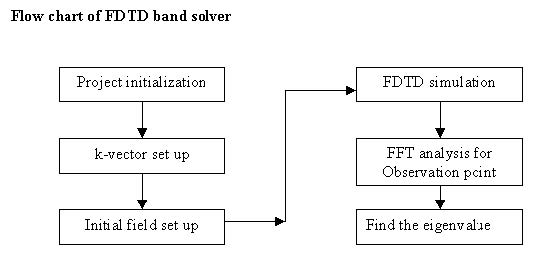
Figure 19: Flow chart of FDTD band solver
Note:
- In OptiFDTD, the FDTD band solver only deals with the 2D square lattice and 2D hexagonal lattice.
- In OptiFDTD, the band solver only accept lossless Isotropic and Anisotropic materials.
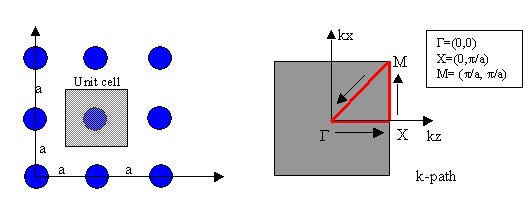
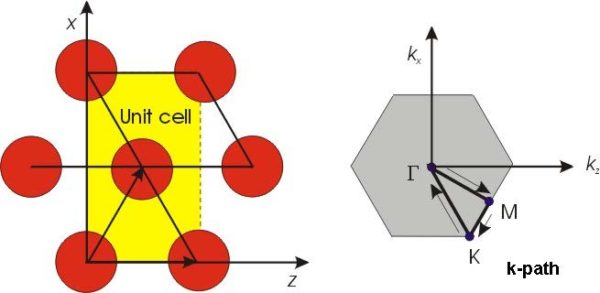
Unit cell and Brillouin zone
The following figures show the unit cell and Brillouin zone in the OptiFDTD
2D FDTD band solver.
Figure 20: Unit cell and associated Brillouin zone for square lattice
Figure 21: Unit cell and Brillouin zone for Hexagonal lattice