By Lorentz dispersion materials, we mean materials for which the frequency
dependence of the dielectric permittivity can be described by a sum of multiple
resonance Lorentzian functions:
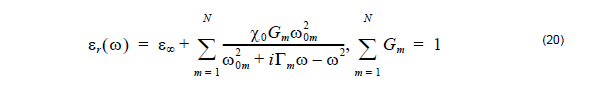
where
| ω0m | are the resonant frequencies |
| Gm | is related to the oscillator strengths |
| Γm | is the damping coefficient |
| ε∞ | is the permittivity at infinite frequency |
| X0 | is the permittivity at ω = 0 . |
In the lossless case Equation 20 is directly related to the Sellmeier equation which in
the three resonances can be presented as:
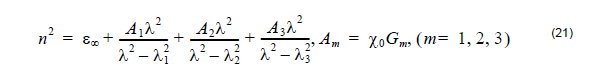
In the lossy case, the Sellmeier equation can be written in a generalized form,
accounting for a non-zero damping coefficient Γm as well as for anisotropy in the
dispersion properties:
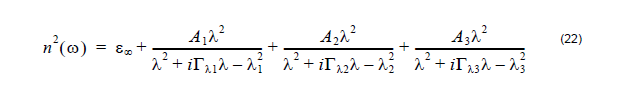
There are different ways to implement Equation 20 into the FDTD formalism. Here we
consider the so-called polarization equation approach in the single resonance case.
It uses the dielectric susceptibility function:
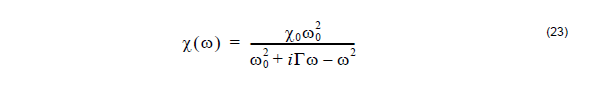
and the relation between the polarization and the electric field Py = ε0x (ω) Ey .
Taking the Fourier transform of the last equation leads to the following differential
equation:
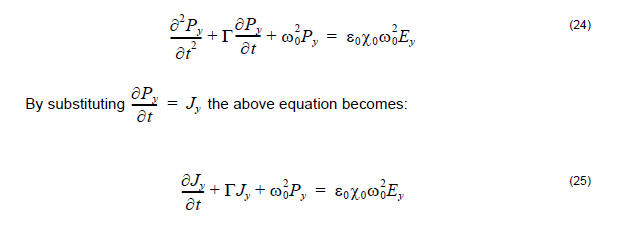
Then Equations 24 and 25 are solved numerically together with the modified Equation
26:
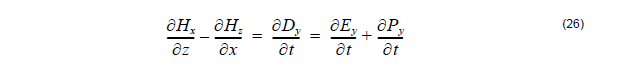
The FDTD approach can also account for a large variety of materials such as Drude
dispersion materials, perfect metal, second-order, and third-order materials.
Lorentz model only supports 2D simulation. Lorentz_Drude material that covers
Lorentz model supports both 2D and 3D simulation.
Drude Model
Drude material in OptiFDTD is marked as
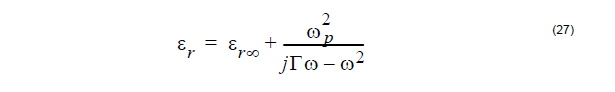
Where εr∞ is the permittivity for infinity frequency, ωp is the plasma frequency, and Γ
is the collision frequency or damping factor.
Drude model only supports 2D simulation, Lorentz_Drude model that covers Drude
model supports both 2D and 3D simulation.

