Assuming ∂ ⁄ ∂z = 0 and regarding n0 as an effective refractive index, Equation 23 is reduced to a basic equation for the guided-mode analysis of anisotropic optical waveguides. Hence, from (9) we get the following Helmholtz equation:
![]()
One can cast the Helmholtz equation into the following matrix form:
![]()
where

and

The differential operators are defined as:
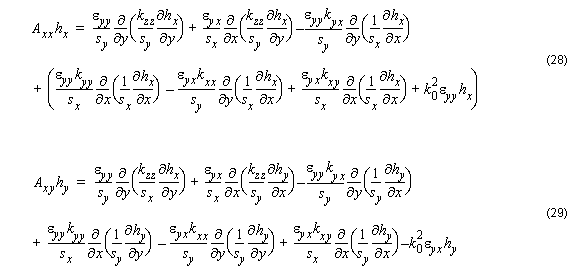
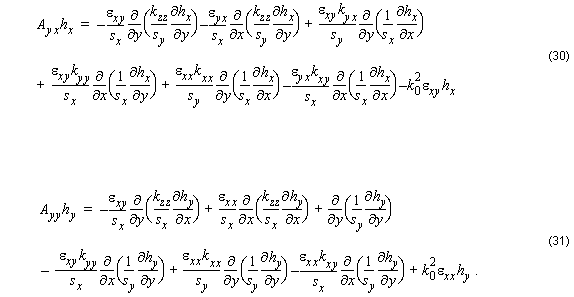
It is noted that in Equations [28] – [31], both the material and the geometrical properties of the waveguides contribute to the polarization dependence,
Axx ≠ Ayy , and coupling:
Axy ≠ 0 and Ayx ≠ 0 .
Like in E-Formulation Equation 25 can be solved by an efficient Arnodi method that takes into account the sparsity under consideration and computes just a few number of eigenvalues and eigenvectors that represent the propagation constants and fields distributions for the wanted modes.

