Using recurrence formula Equation 118 for Padé (3,3), we get:
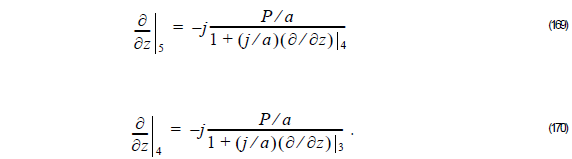
Using Equation 145 into Equation 169, we get:
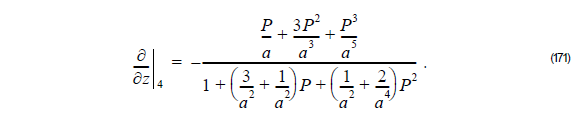
Finally, using Equation 171 into Equation 169, we get:
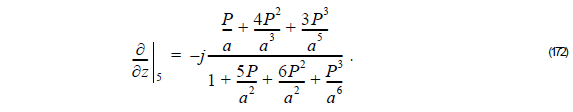
Here a = 2k0nre f .
From Equation 172, we get:
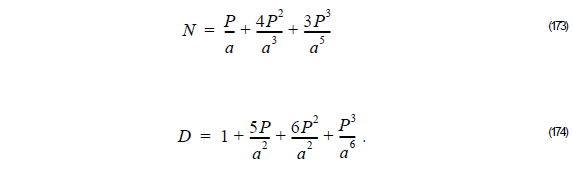
Thus,
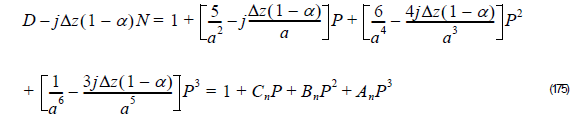
and
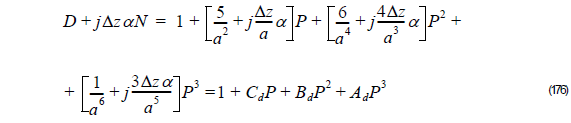
where
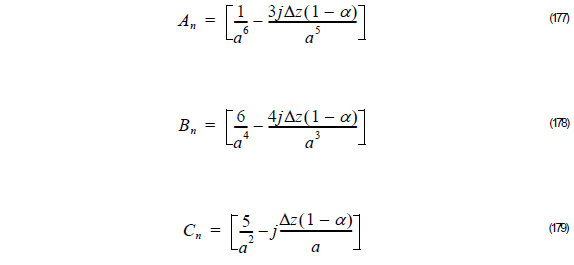
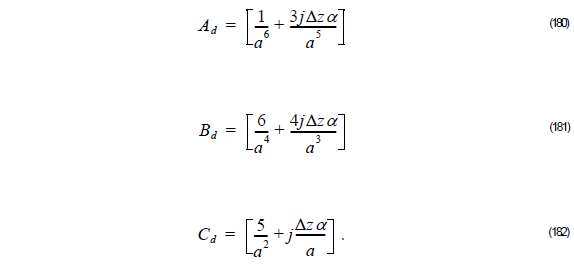
Thus, the unknown field φ l + 1 at z + Δz is related to the known field φ l at z as follows
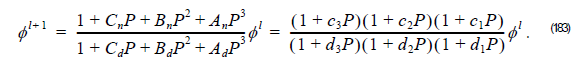
In order to solve Equation 183, we use the Multistep method, that is, the unknown field
φ l + 1 can be obtained from the known field φ l by successively solving Equation 164 for
i = 1, 2, 3 . Therefore for Padé(3,3) we follow the steps:
1 Using φ l , compute φ l + 1 ⁄ 3 considering the linear system:
![]()
In case of using FEM solve,
![]()
2 Using φ l+ 1 ⁄ 3, compute φ l + 2 ⁄ 3 considering the linear system:
![]()
In case of using FEM compute,
![]()
3 Finally, using φ l+ 2 ⁄ 3, compute the following linear system to obtain the unknown field φ l + 1 at z + Δz :
![]()
In case of using FEM compute,
![]()

