The order of the components in the vector f is chosen to help factor the matrix in (9) into two matrices as Ff = Dc where c = [ A, B, C, D ]T ,
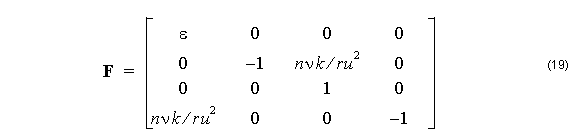
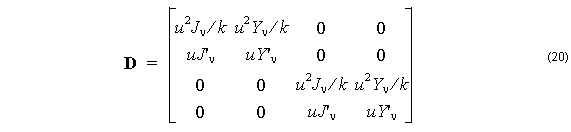
The advantage of this factoring is that it is easy to find the expressions for F–1 and D–1 .
F–1 is found by two row reductions and D–1 by inverting the 2×2 matrices in the block diagonal. These matrices are required to find the coefficients in the next layer. If cm are the coefficients in the m-th layer, then the coefficients in the next layer is found from the matrix product,
![]()
The use of the factored matrix means four matrix multiplications instead of two are required to cross the boundary, but it avoids having to find the matrix inverse numerically.

