Linearly Polarized modes can be found with the same style of approach as above, by a transfer matrix analysis of multilayer fibers.In the LP analysis, the initial excitation is assumed to have a linear polarization, and so a modal analysis supporting only one field component is used. It can be shown this is a good approximation for fibers with low refractive index contrast, as shown below.
Consider again the wave equation of (5), but this time use the vector identity (10) directly on the electric wave equation instead of introducing the Debye potential. The result is
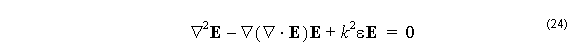
From the Maxwell divergence equation (2)
![]()
so that
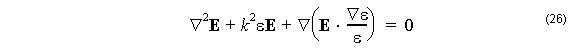
In the case of low index contrast waveguides, such as are found in most optical fibers, the last term in (26) is negligible. The last term is the only one that contributes to coupling among the field components of the electric field, so if this term is neglected, the model will be a polarization preserving model. If the excitation was a linear polarization parallel to the X axis, the model could be further simplified by considering only the X component of (26). This shows that for the LP model, the governing equation for the field is the Helmholtz equation (8) applied to the field component Ex .
The solution for LP modes is constructed in a similar way as for the vector modes. The Ex is constructed in each layer as a linear combination of Bessel functions (16) and (17), except this time only two coefficients, A1 and B1 , are required, since only one function needs to be constructed. The physical consideration at the layer boundaries is the continuity of Ex and its derivative. The two conditions are related to the two coefficients A and B for each layer by 2×2 matrices. The modes are found by setting up a calculation that assumes A1 = 1 and B1 = 0 for the first (inner most) layer, and then calculating the coefficients in each subsequent layer by matrix manipulations. The last layer has the condition that the coefficient ( AM ) of the Bessel function Iν must be zero, since this Bessel function is not bounded at infinity. This last coefficient is a function of the order ν and the modal index n, so the modes are found by finding the zeros of AM ( n ) .

