Implicitly Restarted Arnoldi Method (IRAM)

The repeated application of (10) for every node, and the application of a similar equation for h_y leads to an eigenvector problem of a large system of linear equations. The Finite Difference Mode Solver uses the Implicitly Restarted Arnoldi Method as described in Ref. [2] to find the eigenvectors of this system, and thereby find the modes of the waveguide.
The Implicitly Restarted Arnoldi Method looks for the modes inside a Krylov Subspace. This subspace is constructed from the mode operator, and from an arbitrary (could be random) starting magnetic field, here described as a vector, v₁ . The Krylov subspace

K_m ( Q, v₁ )is the space spanned by powers of the Q when applied to the initial vector v₁ :

The IRAM constructs a basis for the m + 1 dimensional Krylov subspace by the Gram-Schmidt process. For example, a basis for a 2 dimensional Krylov subspace, K₁ ( Q, v₁ ) , can be constructed from v₁ and Q v₁ . A vector perpendicular to  v₁ can be found by subtracting the v₁   component from Qv₁  :

This vector is parallel to the second basis vector, v₂ , which is found once
w₂ is divided by its length,  . It is easy to show that this length is

The above inner product v of with Q occurs frequently, so the matrix components
are defined

With this definition, the effect of including another power of Q can be written in terms
of the new basis vectors

Following the Gram-Schmidt process, a vector in the Krylov subspace that is perpendicular to both v₁ and v₂ can be constructed from subtracting the projections of Qv₂ onto the first two basis vectors

Normalizing w₃ as before, and rearranging terms shows how the space generated

from Q² v₁ can be represented in terms of the basis vectors

The Gram-Schmidt process can be followed in as many steps as necessary to create a basis for the Krylov subspace.

An important point to note is that the dimension of K_m ( Q, v₁ ) , (and therefore the number of basis vectors needed to span it), might be less than m + 1. Let’s suppose that the mode solving problem was asked to find the first k modes, where k < m. Let us also suppose that the initial vector v₁ happened to be a linear combination of these k modes. Modes are solutions to the eigenproblem of equation (11). Let the ith mode field be represented by e_i  , and let its propagation constant (eigenvalue) be β_i²  . Call the subspace spanned by those k modes S_k , to represent a subspace of k dimensions. Then

When the second vector to span the Krylov subspace is calculated, it is apparent it is

also a linear combination of the k eigenvectors, and is therefore still in the subspace, S_k . It is easy to see that this situation is not changed by multiplying by Q again, and so

for any power of Q . (j  can be 1, 2, … up to ∞ ). Therefore the dimension of this Krylov subspace, K_m ( Q, v₁ ) is fewer than the m + 1 vectors in the span (12). For this choice of v₁ , the Krylov subspace has dimension k ( < m), and some of the vectors in (12) have linear dependence on others.

When v₁ is a member of the subspace S_k  , the Gram-Schimdt process must terminate at k, since having m basis vectors is not possible in S_k  . The termination will be seen at the kth step of the process, in trying to calculate a vector perpendicular to the previous k basis vectors. Equation (17) showed the generation of the 3rd vector, the kth will be formed from

When this is done with v₁ ∈ S_k , the w_{k + 1} must be zero, and the Gram-Schmidt process will terminate. Because of the termination, the search for modes will take place in a space of dimension k ( 1, 2, maybe 10) rather than in the space of the vectors themselves. The vectors have dimension equal to the number of nodes in the mesh of Fig. 1. This is typically some number on the order of 105 or 106. This termination greatly simplifies the problem!

Of course, a random choice of v₁ is unlikely to be a member of S_k , but the IRAM strategy is to use iterative processes that effectively change the initial choice of v₁ to a vector inside (or not far from) the subspace S_k .

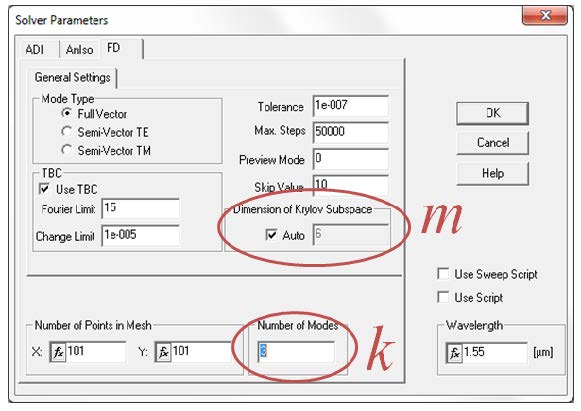
In the FD tab of the Solver Parameters dialog box of OptiMode, both k and m are defined as shown in Fig. 2.

Figure 2: Solver Parameter dialog box of OptiMode displaying the tab for the Finite Difference mode solver (FD). Dimension of Krylov Subspace (m) and number of modes to find (k) are defined here. In the Auto setting, m = 2k with m having a minimum of 4. m can be set by the user by unselecting the Auto check box.

Note that when the Dimension of Krylov Subspace is in its Auto setting, the dimension of the Krylov subspace (m) will be made double the dimension of the number of modes desired (k). In this example, the IRAM will construct a basis for a Krylov subspace of dimension m. This will involve making m copies of the field initially found on the defined mesh. If this mesh is already very large, there is a possibility to create an out-of-memory error, because the mode solver requires at least m times the storage required for a single mode.

The first choice of v₁   will probably not be anywhere near S_k  , so the IRAM begins a process of shifted Q-R iteration to move away from unwanted eigenvalues and closer to the desired ones. When the Q-R iteration process is finished, The algorithm restarts (the R in IRAM). It reduces the dimension of the working space to k, but the new subspace is different because the QR iterations indirectly change the starting vector, v₁ . The result is usually movement toward the desired solution space S_k  .

This leaves a new set of vectors spanning a new k dimensional space, and the algorithm starts the Arnoldi process again to build the dimension up to m. Then another Q-R process will start to move closer to S_k  . See Ref [2] for details. If you watch the computer’s Task Manager while the algorithm runs, you might see the used RAM cycle as the dimension of the space cycles from k to m and back. After many iterations the stopping condition will be met, and at this point the generalization of equation (18) will appear as

If the v₁   is now inside S_k  , the last coefficient in the sum will be zero. This is evident from the definition of h_ij . If v₁   really is inside S_k  , Qv_k is also inside S_k   and it must be perpendicular to v_{k + 1} , making h_{k + 1, K} = 0 . In the practical implementation of the mode solving problem, h_{k + 1, k} won’t be exactly zero, but the IRAM process finishes when it is small enough to be negligible. Once the problem is in the form of (23) with the last term very small, it is easy to find the modes and propagation constants.

To see this, make the following change in notation. Define an n x k matrix columns of which are made from the k Arnoldi basis vectors of size n x 1, V_k  , the v_k

and form a k x k matrix from the hij  coefficients of equation (15). Now consider QVk . Equations (16) and (18) show how the first two columns of QV_k  are formed in terms of h_ij  and the v_k   found in the first three columns of V_k  . The reader can find the following columns by following the Gram-Schmidt process further. Note that H_k  has all zero elements for those below the first subdiagonal, because the ith column of QV_k is a linear combination of the first i + 1 basis vectors v_k . (A matrix of this form is called “Hessian”).

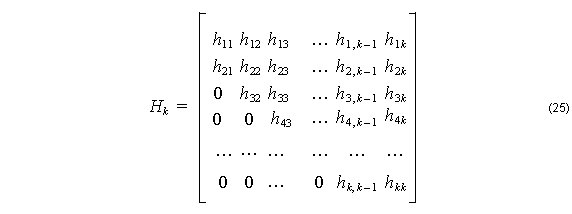
All of the columns of QV_k , except for the last one, are calculated by V_k H_k . The last column (kth column), according to (23) will need to include a term v_{k + 1} . This isn’t available in V_k , so the relation is made complete by adding the last column explicitly:

e_k is the kth unit column vector in a k dimensional space, and the transpose is e_k^T = ( 0, 0, 0, …, 1 ). Putting this row vector after the column vector v_{k + 1} serves to put v_{k + 1} in the last column of a k x k matrix with zeros elsewhere. The second term on the right adds the missing column in the relation. From the above discussion, the h_{k + 1, k} is expected to be small, and it becomes a measure of the accuracy of the solution.

The k modes we are looking for are inside S_k . These modes can be found by finding the eigenvectors of the matrix H_k . This greatly simplifies the problem. The matrix Q is n x n, where n is the number of nodes in the finite difference mesh. n is typically

on the order of 10⁵ or 10⁶. On the other hand H_k is k x k, and k is probably of order of 10 or so. The reduction to (26) simplifies the problem by many orders of magnitude.

The k modes inside S_k are a linear combination of the basis for that space. Let a vector, of size k x 1, s , represent an arbitrary vector in this space

Now let s be an eigenvector of H_k , and let the corresponding eigenvalue be θ .

It is easy to show that, within an accuracy specified by h_k + 1, k , the x
defined in (27) is an eigenvector of Q with eigenvalue θ :

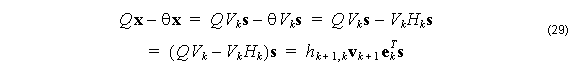
If the last term in (23) is zero, then ( x, θ ) is an exact eigenpair solution for Q . If the last
term is not exactly zero, then the pair ( x, θ ) is called a Ritz Pair, and the norm of (29) is a
measure of how accurately the Ritz Pair approximates the true eigenvector.

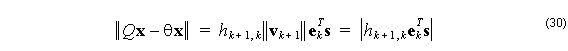
The number the above equation (30) evaluates to is called the Ritz estimate of the
Ritz Pair, ( x, θ ) .

The IRAM will stop when the user specified tolerance has been met, or the maximum number of steps has been exceeded. The tolerance is calculated from the user specified number in the Tolerance field of the Solver Parameters dialog box shown in Fig. 2. The maximum number of steps is from the field called Max. Steps. Letting the tolerance be t , the IRAM will stop when the following condition is met:

where ε_M is the machine precision, or when Max. Steps is exceeded.

When the mode solver is running, while the iterations are taking place, the value in (31) is
exceeded, but it is still informative to observe at least one of the Ritz vectors. In a long
calculation, the user can see if the mode solver is approaching a mode solution or not. If not, the simulation can be stopped, and corrective action taken.

OptiMode calculates one of the Ritz vectors by (27) while the IRAM is going through its iterations. This is the field displayed in the simulator while the calculation is taking place. You can select which Ritz vector to view with the entry in the field Preview Mode field in the Solver Parameters dialog box (Fig. 2). Selecting 0 in this field will calculate and display the first Ritz vector, the current approximation to the fundamental mode. Entering 1 in this field will calculate and display the second Ritz vector, an approximation to the next higher mode, and so on. The fields don’t change very much from one iteration to the next, so to save execution time you might not want to calculate and view a Ritz vector for every iteration. If you want to observe every 10th iteration, enter 10 in the Skip Value field.