Using recurrence formula Equation 118 for Padé(2,2) we get:
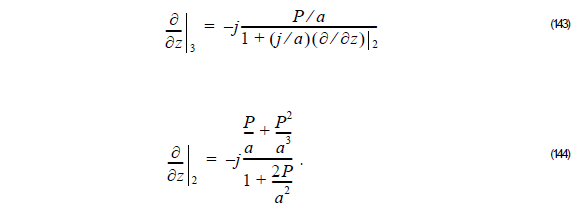
Here a = 2k0nref .
Using Equation 144 into Equation 143, we get:
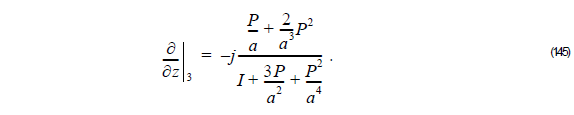
From Equation 145, we get:
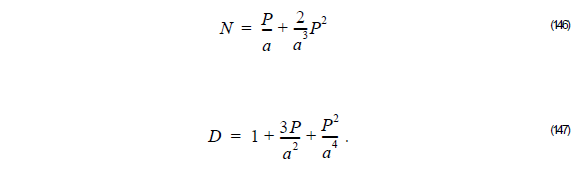
Thus,
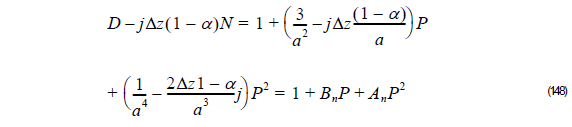
and,
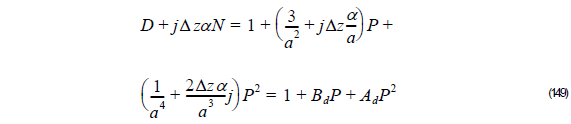
where:
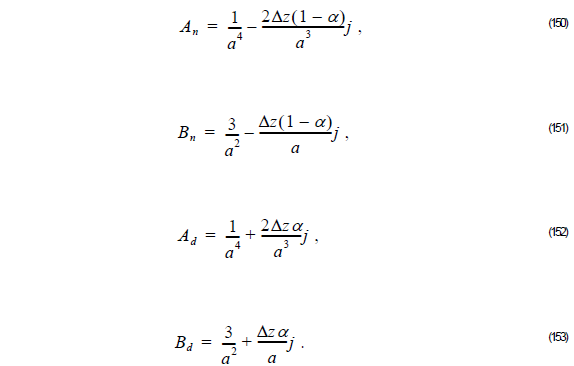
Thus, the unknown field φ l + 1 at z + Δz is related to the known field φ l at z as follows:
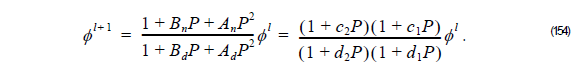
Multistep Method
In order to solve Equation 154, we applied the multistep method developed by Hadley.
First, we rewrite Equation 154 as
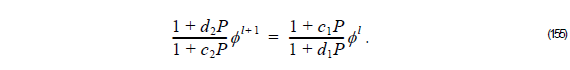
Then, defining the field φ l + 1 ⁄ 2 as
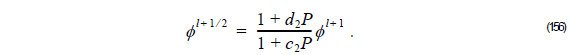
We rewrite Equation 154 as
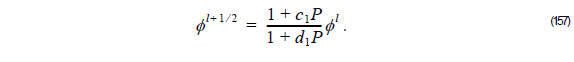
Since φ l is known, we can obtain φ l + 1 ⁄ 2 by solving:
![]()
If we consider FEM, we get,
![]()
Thus, we can rewrite Equation 158 as
![]()
here
![]()
Using φ l + 1 ⁄ 2 , we rewrite Equation 156 as
![]()
If we are using FEM, we get,
![]()
Solving Equation 162 or Equation 162, we can obtain the unknown field φ l + 1 . It is apparent from the form of Equation 154 that an n th-order Padé propagator may be decomposed into an n -step algorithm for which the i th partial step takes the form
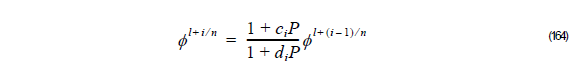
when i = 1, 2, …, n .
The run time for an n th-order propagator is obviously n times the paraxial run time. Therefore, for Padé (2,2) we follow the steps:
1 Compute φ l + 1 ⁄ 2 considering the linear system:
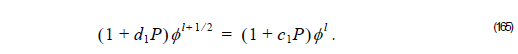
If we are using FEM we get:
![]()
2 Finally, to get the field φ l + 1 at z + Δz we solve:
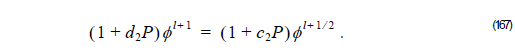
If we are using FEM, we get,
![]()

