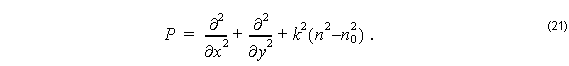The above system of equations for BPM is called the Full-Vector form, as it includes both transverse components of the field. Often it is not necessary to have both field components in the simulation. If it is known that the device does not change the polarization of light, then it is sufficient to model one polarization at a time (or only model the expected polarization). In these cases the contribution of ey to ex and vice versa can be ignored, and the governing equation is
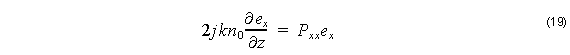
for Semi-Vector TE and
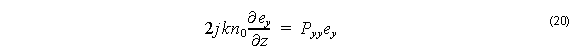
for Semi-Vector TM. In Semi-Vector BPM, one can notice a difference in the propagation of light depending on whether the initial light is polarized parallel or perpendicular to the device substrate. However, once polarized horizontally, for example, the model does not allow the horizontal light to transfer into a vertical polarization.
On the other hand, for structures with a very low index contrast, it won’t make much difference in the order of application of operators like ∂ ⁄ ∂x and n2 . In this case, the operators commute, and both Pxx and Pyy reduce to the scalar operator: