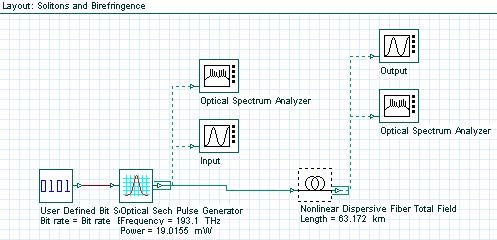
This lesson demonstrates that the Kerr nonlinearity, which stabilizes solitons against spreading due to GVD, also stabilizes them against splitting due to birefringence [1] – [3].
The “single-mode” fibers are actually bimodal because of the presence of birefringence. This means that the group velocity is different for pulses polarized along the two principal axes.
If the pulse contains both polarization components, in addition to spreading due to GVD, the partial pulses will tend to split apart because of birefringence [1], [2].
In the anomalous GVD regime, the Kerr nonlinearity can compensate the spreading due to GVD, leading to formation of a soliton. The similar fact is true for the birefringent walk-off.
Above a certain soliton number, which increases with the strength of the linear birefringence, the two polarizations interact to form a soliton consisting of both polarizations. The physical effect responsible for this type of behavior is the cross-phase modulation between the two polarization components.
Mathematically [1], [2], the propagation of a pulse in linear birefringent fiber, in the absence of loss, with an arbitrary polarization with respect to the principal polarization axes is described by the following system of coupled NLS equations:
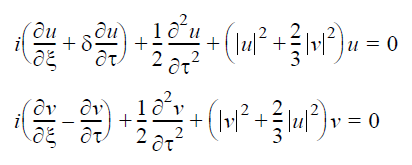
In Equation 1
![]()
is the normalized group velocity mismatch between the two polarization components.
![]()
is the normalized time, where
is inversely related to the average group velocity, and
![]()
The electric field envelopes are normalized according to
![]()
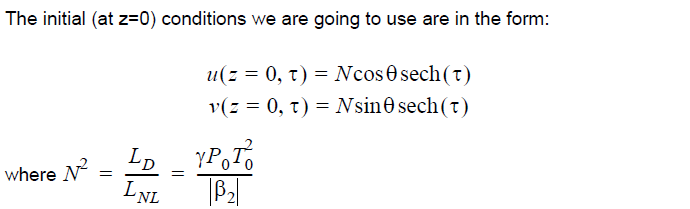
is the soliton number (see “Self-phase modulation and group velocity dispersion” from
the Tutorials). The layout is shown in Figure 1.
Figure 1: Solitons and birefringence layout
We set the bit rate to 10 Gb/s and the pulse width to 0.5 bit (50 ps).
![]()
(corresponding to 1550 nm, in the anomalous GVD regime of the fiber), the power
necessary to launch the fundamental soliton is P0 = 19.0155 mW and the soliton
period is Z0 = 63.172km.
We set the value of the birefringence to Δn = nx – ny = 2.1187 x 10-7, where nx and ny are the effective mode indices for x and y polarized components respectively.
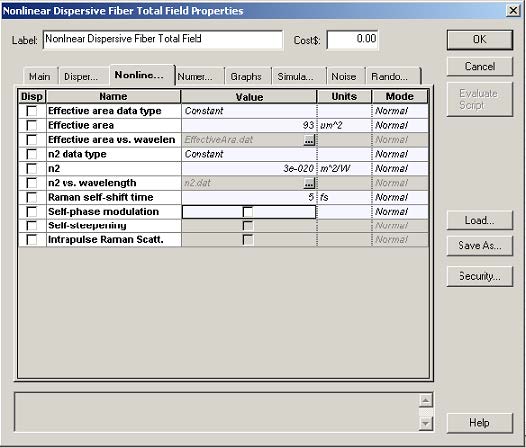
The difference in the group delays per unit fiber length between both polarization components is then Δn / c = 0.7067ps / km . Since T0 = 28.3607 ps , the value of the group velocity mismatch parameter δ is δ = 0.5 . To see the birefringence- induced time delay between both polarization components, we set azimuth in the optical sech pulse generator equal to 45° , fiber length to 631.72 km (10 soliton periods) and switch the nonlinear effects OFF (see Figure 2).
Figure 2: Fiber parameters
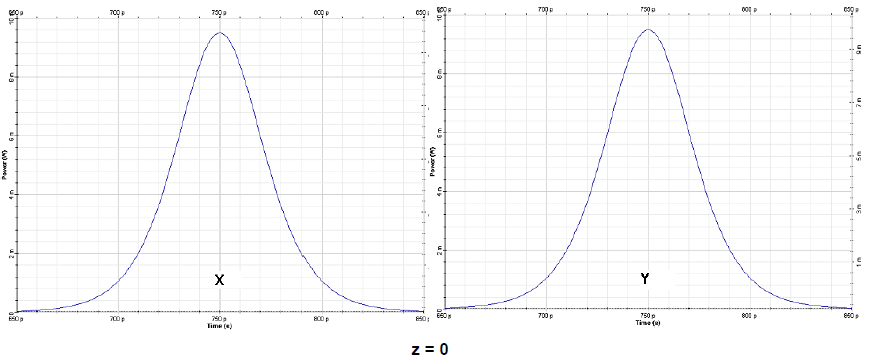
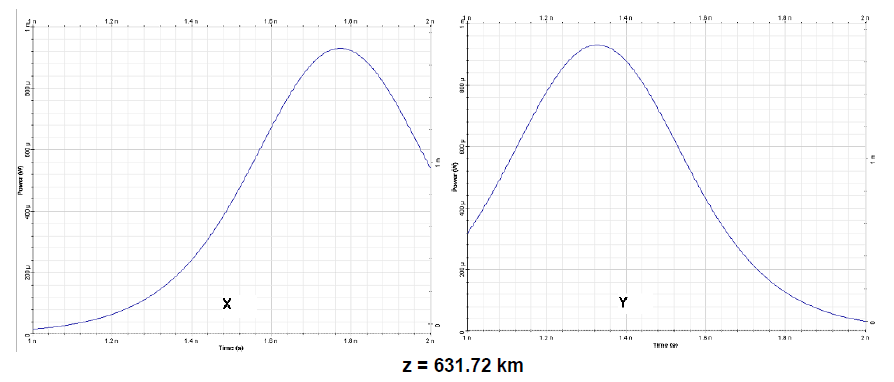
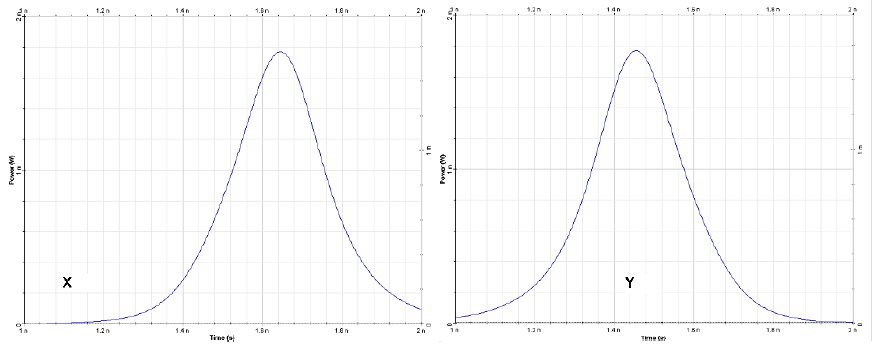
Figure 3(a) shows the input and output partial pulses after 631.72 km propagation in a loss-free fiber. Both partial pulses are broadened by GVD and shifted in time by 440 ps with respect to each other, which corresponds to a difference in the arrival times of 0.7 ps for 1 km of fiber length. This shift can be attributed to the birefringence.
Figure 3 (a): Input polarization components x (left) and y (right) for a sech-pulse in linear regimez
Figure 3(b): Output polarization components x (left) and y (right) for a sech-pulse in linear regime
When the nonlinearity is taken into account, the two polarization components remain bound together if N in Equation 2 exceeds some critical value Nth that increases with the increase δ. For δ = 0.5, this value is [1], [2] Nth ≈ 1.
To see this, we switch the nonlinear effects ON in the fiber component. The output pulses for 631.72 km of propagation are shown in Figure 4.
Figure 4: Partial pulses after propagating in 631 km of fiber taking into account the nonlinear effects
Comparing Figure 4 and Figure 3(a), we can see that the impact of the nonlinearity is twofold: Nonlinear effects reduce the GVD induced pulse broadening for each of the polarization components, and the time delay between both is reduced with respect to case of linear propagation (i.e. neglecting the nonlinear effects, Figure 3(a)).
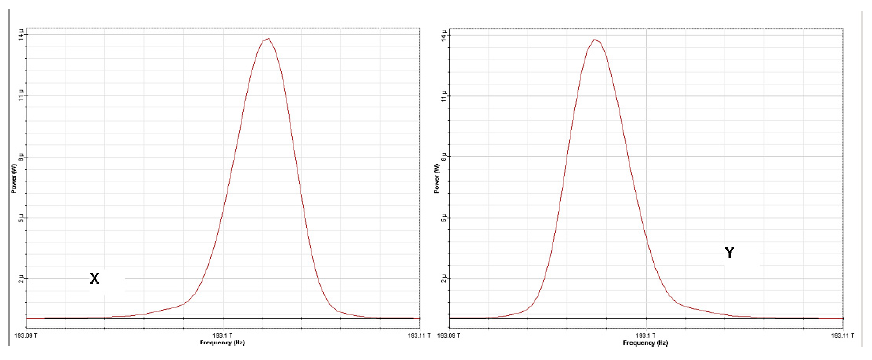
Figure 5(a): Input pulse spectra evolution over 10 soliton periods x (slow axis) and y (fast axis)
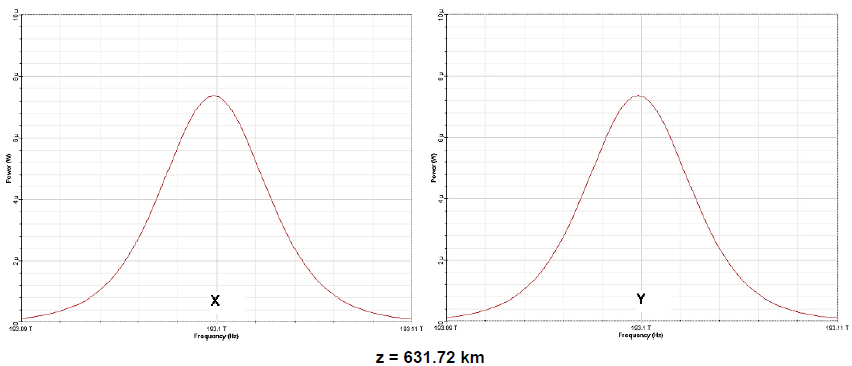
Figure 5(b): Output pulse spectra evolution over 10 soliton periods x (slow axis) and y (fast axis)
When the nonlinear effects are taken into account, the time delay is roughly 200 ps, which is more than a factor of two smaller compared to the case of linear-regime propagation. It can be concluded that Kerr nonlinearity reduces the birefringent walk-off [2].
To understand this phenomenon in somewhat more detail, we can look at the evolution of the pulse spectra corresponding to the pulse shapes presented in Figure 4. The spectra are presented in Figure 5(a) and Figure 5(b).
Initially the spectra for both x (slow) and y (fast) polarization components are identical. However, due to the action of the cross-phase modulation between both polarization components, the spectrum of the x-polarization component acquires a blue shift, while the spectrum of the y-polarization component turns out to be red-shifted.
In the case of the anomalous GVD considered here, the high frequency (blue) components travel faster than the low frequency (red) components.
Hence, as a result of the action of the cross-phase modulation between both polarization components (the last terms in the system Equation 1), the faster polarization component is slowed down while the slower polarization component is accelerated and consequently the birefringent walk-off is reduced.
When ∅ ≠ 45° in Equation 2, the two components have different amplitudes initially.
In this case, when N exceeds Nth, the evolution scenario is qualitatively different,
depending on the value of the birefringence ( δ -parameter in Equation 1). With
∅ = 30°, this is illustrated in Figure 6 and Figure 7 for different values of the
birefringence.
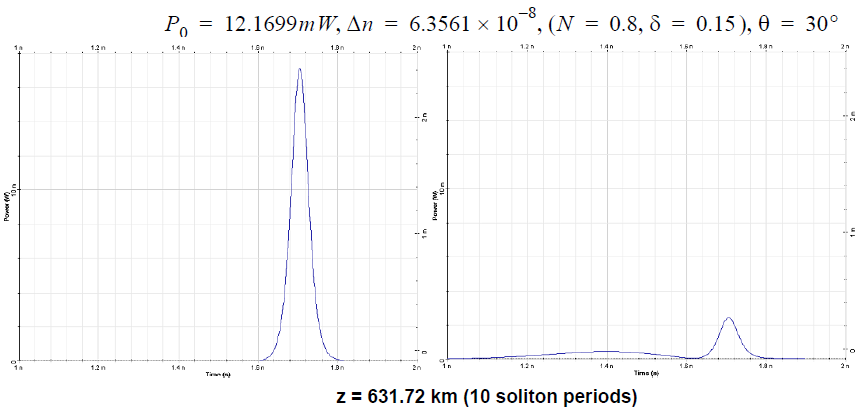
For the case δ = 0.15, (Figure 6), the smaller pulse is captured by the larger and two move together. However, when δ = 0.5, the larger one captures a fraction of the energy in the smaller pulse and the rest of it is dispersed with propagation.
The results shown in Figure 6 and Figure 7 indicate that under certain conditions the two orthogonally polarized components of the soliton move with a common group velocity despite of their different modal indices. This phenomenon is known as soliton trapping [3].
Figure 6: Pulse evolution over 20 soliton periods for:
References:
[1] C. R. Menyuk, Opt. Lett., 12, p. 614 (1987).
[2] C. R. Menyuk, JOSA B, 5, p. 392(1988).
[3] G. P. Agrawal Nonlinear Fiber Optics, Academic Press (2001).