For finding electromagnetic fields in a cylindrical geometry it is convenient to use cylindrical coordinates r, θ and z, and Debye potentials parallel to the axis of rotation, ![]() [2]
[2]
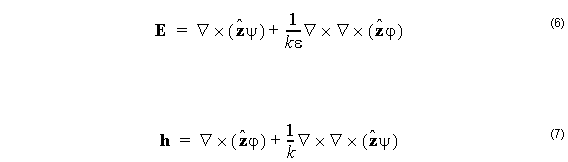
It is supposed that the permittivity is constant in the region in which the above equations apply. The fibers are defined as a series of concentric layers of constant dielectric, so for the fiber mode solver, the region is the annulus between the layer boundaries. Equation 6 and Equation 7 are applied in a piecemeal way. Strictly speaking, the ψ , ϕ and ε should have subscripts to indicate to which layer the solution applies, but they are dropped here to simplify the representation. The complete solution for the multilayer fiber will be constructed by using a separate pair of functions for each layer, and by matching the tangential field components at the layer boundaries.
The divergence of the curl of any vector field is identically zero. Therefore the choice of (6) and (7) to represent the electric and magnetic fields means that the divergence equations (2) will automatically be satisfied. In the remainder of this section, we show that if the two potentials ψ and ϕ are solutions to the scalar Helmholtz equation, then (6) will be a solution to the Maxwell wave equation (5), at least within any given layer. In subsequent sections, the particular solution for the mode will be found by observing the boundary conditions imposed by physical considerations on E and h.
Suppose ψ is a continuous function of position that satisfies the Helmholtz equation in 3 dimensions
![]()
Consider the following equation, true for any ψ satisfying (9) in a region of constant
permittivity.
![]()
Associate the first two terms together and apply the vector identity
![]()
to get
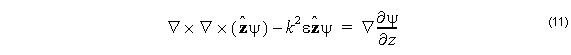
The right hand side of (11) is a gradient of a scalar function, so the curl of the left hand side must be zero. take the curl of (11)
![]()
and define E by the first term of (6). With E defined this way, the Maxwell electric wave equation (5) follows, and therefore this E is a possible solution for electric field.
Solutions defined from the ψ function solely (that is to say, solutions with ϕ = 0), will have
electric fields of the form
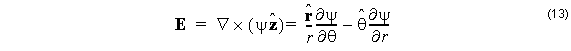
from which we can see there is no longitudinal (z) component to the electric field, i.e.
these are transverse electric fields. The magnetic field associated with these
transverse electric fields is constructed from the first Maxwell curl equation in (4):
![]()
which is the second term of (7). The same sequence (7) – (11) can be applied to the ϕ function to give transverse magnetic fields, and the electric components of these are given as the second term of (6). A linear superposition of transverse magnetic and transverse electric fields will give solutions that are neither transverse magnetic nor transverse electric. In fact, most modes of the fiber are of this hybrid kind. In the hybrid case, equations (6) and (7) are used as written, and the relative value of the ψ and ϕ is
now important, since it is a specific linear combination that matches the boundary conditions at the layer boundaries.

