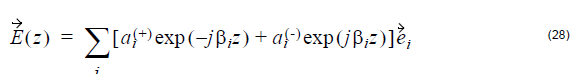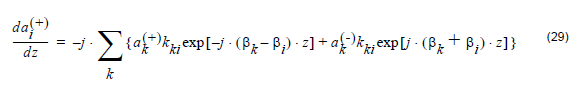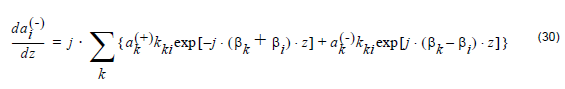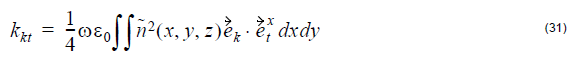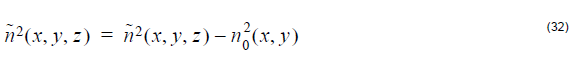Coupled Mode Equations

Assume the electric field is a linear combination of the ideal modes (with no grating
perturbation), such that

where a_i⁽⁺⁾ and a_i^(-) are the slowly varying amplitudes of ith mode traveling in the +z
and –z directions. β_i and is the propagation constant and modal field of the ith
mode.

The above electric field is used as trial solution in the Maxwell’s equation. The
following Coupled mode Equations (CMEs) can be derived by using the properties of
waveguide modes,

The coupling coefficient between modes k and i is given by:

where  is the periodic refractive index perturbation of the grating,
and n₀(x, y) is the index profile of waveguide. n(x, y, z) is the grating index profile.

In OptiGrating, the coupled mode equations are based on non-orthogonal coupled
mode theory. Both the waveguide nature coupling and grating coupling are
considered. In order to formulate the coupled mode equations, waveguide modal
constants, fields, and coupling coefficients are calculated based on waveguide and
grating profiles. The coupled mode equations are then solved by the two mode or by
the multi-mode coupling formulation.