The potentials themselves are solutions of the scalar Helmholtz equation, and the particular solution is found by observing the boundary conditions imposed by physical considerations on E and h. The potentials are supposed to form modes, so a solution where the variables are separated is appropriate
![]()
and a similar expression applies for the other Debye potential, ϕ . The Helmholtz equation (8) is expanded in cylindrical co-ordinates, and then (15) is substituted.For regions where ε is constant, the radial functions follow the Ordinary or Modified Bessel equation, and so the solutions are linear combinations of Bessel functions of integer order v. In any given layer,
![]()
where ![]() . In layers where the propagation constant squared is larger than k2ε , the Bessel functions J and Y are replaced by the Modified Bessel functions I and K, respectively.,
. In layers where the propagation constant squared is larger than k2ε , the Bessel functions J and Y are replaced by the Modified Bessel functions I and K, respectively.,
![]()
where ![]() . Equations (15), (16), and (17) are substituted in (6) and (7) to find the electromagnetic fields. It is the tangential components θ and z that are needed explicitly, since it is the tangential components of the electric and magnetic fields that should match at layer boundaries. These field components are related to the coefficients A, B, C, and D by a 4×4 matrix.
. Equations (15), (16), and (17) are substituted in (6) and (7) to find the electromagnetic fields. It is the tangential components θ and z that are needed explicitly, since it is the tangential components of the electric and magnetic fields that should match at layer boundaries. These field components are related to the coefficients A, B, C, and D by a 4×4 matrix.
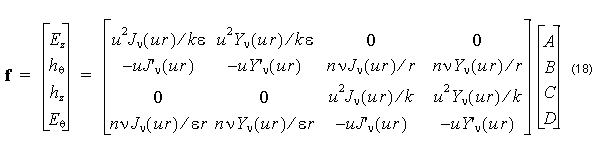
where n = β ⁄ k is the modal index, and the common factor exp [ j( νθ – βz ) ] is suppressed. In layers where the propagation constant squared is larger than k2ε , the Bessel functions J and Y are replaced by the Modified Bessel functions I and K, respectively, and the u is replaced by w.
A similar equation to (18) applies in adjacent layers, with different constants A, B, C, D. Given the constants in one layer, the constants in the adjacent layer can be found by solving the linear system created by the field matching condition. The f found by the two matrices should be the same field vector at the boundary between layers. The difference between this formulation and that in Ref. [2] and [3] is that this formulation uses real numbers only.

